题目内容
1.在Rt△ACB中,∠C=90°,AC=1,BC=2,则sinB的值为( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
分析 根据勾股定理求出斜边AB的值,在利用正弦的定义直接计算即可.
解答 解:在Rt△ACB中,∠C=90°,AC=1,BC=2,
∴AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴sinB=$\frac{AC}{AB}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
故选B.
点评 本题主要考查锐角三角函数的定义,解决此类题时,要注意前提条件是在直角三角形中,此外还有熟记三角函数是定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列不适合全面调查的是( )
| A. | 老师检查全班同学完成作业情况 | |
| B. | 人口普查 | |
| C. | 汽车公司检测安全气囊在撞击时的保护作用 | |
| D. | 机场安检 |
9.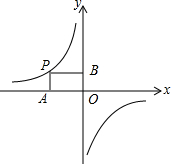 如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )
如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )
 如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )
如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )| A. | 24 | B. | 12 | C. | -24 | D. | -12 |
16.下列y关于x的二次函数y=nx2-2x-n(n>0)的图象与x轴的交点的判断中,正确的是( )
| A. | 没有交点 | |
| B. | 只有一个交点,在x轴的负半轴上 | |
| C. | 有两个交点,都在x轴的正半轴 | |
| D. | 有两个交点,分别在x轴的正、负半轴上 |
6.函数y=$\frac{1}{x}$中自变量x的取值范围是( )
| A. | x≠1 | B. | x≠0 | C. | x>0 | D. | 全体实数 |
10.如图,在边长为a的正方形的右下角,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个平行四边形,这一过程可以验证一个关于a,b的等式为( )
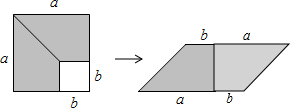

| A. | (a-b)2=a2-2ab+b2 | B. | a2+ab=a(a+b) | C. | (a+b)2=a2+2ab+b2 | D. | a2-b2=(a+b)(a-b) |
11.随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查发现,截至2016年底某市汽车拥有量为16.9万辆,已知2014年底该市汽车拥有量为10万辆,设2014年底至2016年底该市汽车拥有量的年平均增长率为x,根据题意可列方程得( )
| A. | 10(1-x)2=16.9 | B. | 10(1+2x)=16.9 | C. | 10(1+x)2=16.9 | D. | 16.9(1+x)2=10 |
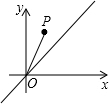 如图,在平面直角坐标系中,点P的坐标为(1,2),将线段OP沿y轴正方向移动m(m>0)个单位长度至O′P′,以O′P′为直角边在第一象限内作等腰直角△O′P′Q,若点Q在直线y=x上,则m的值为2或3.
如图,在平面直角坐标系中,点P的坐标为(1,2),将线段OP沿y轴正方向移动m(m>0)个单位长度至O′P′,以O′P′为直角边在第一象限内作等腰直角△O′P′Q,若点Q在直线y=x上,则m的值为2或3.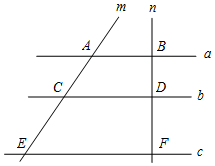 如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,AE=10,BD=3,则DF的值是( )
如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,AE=10,BD=3,则DF的值是( )