题目内容
4. 如图,在⊙O中.弦AB,CD相交于点E,若AE=BE=3,CE=2,则CD的值为$\frac{13}{2}$.
如图,在⊙O中.弦AB,CD相交于点E,若AE=BE=3,CE=2,则CD的值为$\frac{13}{2}$.
分析 根据相交弦定理列出等积式,求出DE,计算即可.
解答 解:由相交弦定理得,AE•EB=CE•DE,
即3×3=2×DE,
解得,DE=$\frac{9}{2}$,
∴CD=CE+DE=$\frac{13}{2}$,
故答案为:$\frac{13}{2}$.
点评 本题考查的是相交弦定理的应用,掌握圆内的两条相交弦,被交点分成的两条线段长的积相等是解题的关键.

练习册系列答案
相关题目
15.关于线段的垂直平分线有以下说法:①一条线段的垂直平分线的垂足,也是这条线段的中点.②线段的垂直平分线是一条直线.③一条线段的垂直平分线就是这条线段的对称轴.其中正确的说法( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无 |
12.下列不适合全面调查的是( )
| A. | 老师检查全班同学完成作业情况 | |
| B. | 人口普查 | |
| C. | 汽车公司检测安全气囊在撞击时的保护作用 | |
| D. | 机场安检 |
9.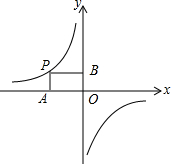 如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )
如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )
 如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )
如图,点P在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,过点P分别作PA⊥x轴于点A,PB⊥y轴于点B,若四边形PAOB的面积为12,则k的值为( )| A. | 24 | B. | 12 | C. | -24 | D. | -12 |
16.下列y关于x的二次函数y=nx2-2x-n(n>0)的图象与x轴的交点的判断中,正确的是( )
| A. | 没有交点 | |
| B. | 只有一个交点,在x轴的负半轴上 | |
| C. | 有两个交点,都在x轴的正半轴 | |
| D. | 有两个交点,分别在x轴的正、负半轴上 |
14.下列关于相似的命题中,①等边三角形都相似;②直角三角形都相似;③等腰直角三角形都相似;④矩形都相似,其中真命题有( )
| A. | ①② | B. | ①③ | C. | ①③④ | D. | ①②③④ |
 有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1>0,一定成立的有( )
有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1>0,一定成立的有( )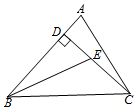 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=10,DE=3,则△BCE的面积等于( )
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=10,DE=3,则△BCE的面积等于( )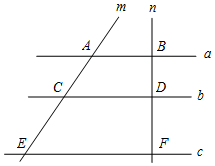 如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,AE=10,BD=3,则DF的值是( )
如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,AE=10,BD=3,则DF的值是( )