题目内容
20.化简求值:[x(x2y2-xy)-y(x2-x3y)]÷3x2y,其中xy=$\frac{3}{2}$.分析 先运用乘法的分配律和去括号法则,对括号内的整式进行化简,然后通过因式分解和约分将原式进行化简,最后把xy=$\frac{3}{2}$代入化简后的代数式即可.
解答 解:当xy=$\frac{3}{2}$时,
原式=(x3y2-x2y-x2y+x3y2)÷3x2y
=(2x3y2-2x2y)÷3x2y
=2x2y(xy-1)÷3x2y
=$\frac{2}{3}$(xy-1)
=$\frac{2}{3}$×($\frac{3}{2}$-1)
=$\frac{2}{3}$×$\frac{1}{2}$
=$\frac{1}{3}$.
点评 本题主要考查了乘法的分配律、去括号法则、因式分解、约分等知识,需要注意的是:括号前是减号,去括号时,括号内的每一项都要变号.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
5.下列计算正确的是( )
| A. | (-2a2b3)÷(-2ab)=a2b2 | B. | (3x2y-6xy)÷6xy=0.5x | ||
| C. | (21x5y2-9x4y3)÷3x3y2=7x2-3xy | D. | (3x2y+xy)÷xy=3x |
10.代数式-$\frac{3}{5}{x}^{2}{y}^{3}$的系数是( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -3 | D. | -5 |

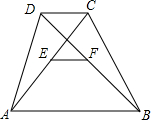 已知:如图,在四边形ABCD中,AB∥CD,AB>CD.E、F分别是AC、BD的中点.
已知:如图,在四边形ABCD中,AB∥CD,AB>CD.E、F分别是AC、BD的中点.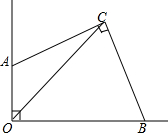 如图,若∠AOB=∠ACB=90°,OC平分∠AOB.
如图,若∠AOB=∠ACB=90°,OC平分∠AOB.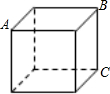 如图,一只蚂蚁要从正方体得一个顶点A沿表面爬行到顶点B,则沿线段AB爬行,就可以爬行路线最短,这其中的道理是两点之间,线段最短.
如图,一只蚂蚁要从正方体得一个顶点A沿表面爬行到顶点B,则沿线段AB爬行,就可以爬行路线最短,这其中的道理是两点之间,线段最短.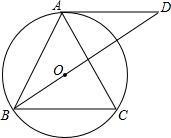 如图,△ABC中,AB=AC,⊙O为△ABC的外接圆,延长BO交⊙O的切线于D,求证:AD∥BC.
如图,△ABC中,AB=AC,⊙O为△ABC的外接圆,延长BO交⊙O的切线于D,求证:AD∥BC.