题目内容
11.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( )| A. | m>2 | B. | m>0 | C. | m>-1 | D. | -1<m<0 |
分析 由抛物线解析式可求得其顶点坐标,由顶点坐标所在的象限可得到关于m的不等式组,可求得m的取值范围.
解答 解:
∵y=(x-m)2+(m+1),
∴抛物线顶点坐标为(m,m+1),
∵顶点坐标在第一象限,
∴$\left\{\begin{array}{l}{m>0}\\{m+1>0}\end{array}\right.$,解得m>0,
故选B.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为直线x=h,顶点坐标为(h,k).

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
19.如果|a+2|+(b-1)2=0,那么(a+b)2016的值是( )
| A. | -2009 | B. | 2009 | C. | -1 | D. | 1 |
1. 一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )
一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )
 一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )
一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )| A. | 165° | B. | 150° | C. | 135° | D. | 145° |
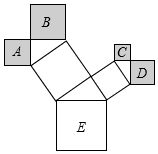 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是3、5、2、3,则最大正方形E的面积是( )
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是3、5、2、3,则最大正方形E的面积是( )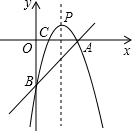 如图,直线y=x-3与x轴、y轴分别相交于点A,B,经过A,B两点的抛物线y=-x2+bx+c与x轴的另一个交点为C.
如图,直线y=x-3与x轴、y轴分别相交于点A,B,经过A,B两点的抛物线y=-x2+bx+c与x轴的另一个交点为C.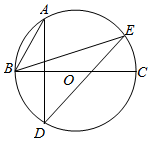 如图,BC为⊙O的直径,弦AD⊥BC,若sinE=$\frac{3}{7}$,BC=7cm,则AB的长为$\frac{49}{41}$cm.
如图,BC为⊙O的直径,弦AD⊥BC,若sinE=$\frac{3}{7}$,BC=7cm,则AB的长为$\frac{49}{41}$cm.