题目内容
16.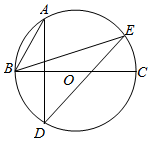 如图,BC为⊙O的直径,弦AD⊥BC,若sinE=$\frac{3}{7}$,BC=7cm,则AB的长为$\frac{49}{41}$cm.
如图,BC为⊙O的直径,弦AD⊥BC,若sinE=$\frac{3}{7}$,BC=7cm,则AB的长为$\frac{49}{41}$cm.
分析 连接OA,设AD与BC交于点F,由圆周角定理可知:∠E=∠BAD,所以sin∠BAD=sin∠E=$\frac{3}{7}$,设BF=3x,AB=7x,根据勾股定理求出x的值即可.
解答  解:连接OA,设AD与BC交于点F,
解:连接OA,设AD与BC交于点F,
由圆周角定理可知:∠E=∠BAD,
∴sin∠BAD=sin∠E=$\frac{3}{7}$
设BF=3x,AB=7x,
由勾股定理可知:AF2=40x2,
∵OA=OB=$\frac{1}{2}$BC=$\frac{7}{2}$,
∴OF=$\frac{7}{2}$-3x,
∴由勾股定理可知:OA2=OF2+AF2,
∴$\frac{49}{4}$=($\frac{7}{2}$-x)2+40x2,
∴解得:x=$\frac{7}{41}$,
∴AB=7x=$\frac{49}{41}$
故答案为:$\frac{49}{41}$
点评 本题考查圆周角定理,涉及勾股定理,圆周角定理,锐角三角函数,解题的关键是根据sin∠BAD=sin∠E=$\frac{3}{7}$,设BF=3x,AB=7x,利用勾股定理求出x的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列各组图形中,属于全等图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( )
| A. | m>2 | B. | m>0 | C. | m>-1 | D. | -1<m<0 |
5.若不等式$\left\{\begin{array}{l}{x-b<0}\\{x+a>0}\end{array}\right.$的解集为2<x<3,则a,b的值为( )
| A. | -3,2 | B. | 2,-3 | C. | 3,-2 | D. | -2,3 |
6.已知一元二次方程ax2+bx+c=0,若a+b+c=0,则该方程一定有一个根为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
 如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,则∠BAP=30°.
如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,则∠BAP=30°.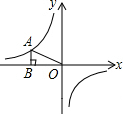 如图,点A为反比例函数y=-$\frac{4}{x}$图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为2.
如图,点A为反比例函数y=-$\frac{4}{x}$图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为2.