题目内容
3.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式为y=-1.5x2+60x,该型号飞机着陆后滑行600m才能停下来.分析 根据题意可知,要求飞机着陆后滑行的最远距离就是求y=-1.5x2+60x的最大函数值,将函数解析式化为顶点式即可解答本题.
解答 解:∵y=-1.5x2+60x=-1.5(x-20)2+600,
∴x=20时,y取得最大值,此时y=600,
即该型号飞机着陆后滑行600m才能停下来,
故答案为:600.
点评 本题考查二次函数的应用,解答此类问题的关键是明确题意,会求二次函数的最值.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
11.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( )
| A. | m>2 | B. | m>0 | C. | m>-1 | D. | -1<m<0 |
13.巴黎与北京的时差为-7小时(正数表示同一时刻比北京时间早的时数),如果北京时间11月11日14:00,那么巴黎时间是( )
| A. | 11月11日21时 | B. | 11月11日7时 | C. | 11月10日7时 | D. | 11月11日5时 |
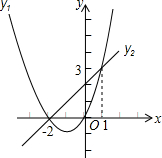 如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2<y1时,x的取值范围x>1或x<-2.
如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2<y1时,x的取值范围x>1或x<-2. 一次函数y=kx+b的图象如图所示,若y>0,则x的取值范围是x<-2.
一次函数y=kx+b的图象如图所示,若y>0,则x的取值范围是x<-2.