题目内容
2.德国著名数学家高斯在上小学时,有一次老师让同学计算“从1到100这100个正整数的和”,许多同学都采用了依次累加的计算方法,计算起来非常烦琐,且易出错.聪明的小高斯经过探索后,给出了下面漂亮的解答过程.解:设S=1+2+3+…+100,①
则S=100+99+98+…+1.②
①+②,得
2S=101+101+101+…+101.
所以2S=100×101,
S=$\frac{1}{2}$×100×101=50×101=5050
所以1+2+3+…+100=5050.
后来人们将小高斯的这种解答方法概括为“倒序相加法”.
阅读上面扥文字,解答下面的问题:
(1)请你运用高斯的“倒序相加法”计算:1+2+3+…+200.
(2)请你运用高斯的“倒序相加法”计算:1+2+3+…+n.
(3)请你利用(2)中的结论计算:1+2+3+…+2000.
分析 (1)通过观察可知,题目中的加数构成一个公差为1的等差数列,则本题根据高斯求和的有关公式计算即可;
(2)根据等差数列和=(首项+末项)×项数÷2,即可解答;
(3)根据(2)中的规律,即可解答.
解答 解:(1)1+2+3+4+5+…+200
=(1+200)×200÷2
=201×200÷2
=20100.
(2)1+2+3+…+n
=(1+n)•n÷2
=$\frac{n(n+1)}{2}$.
(3)1+2+3+…+2000
=$\frac{2000×(2000+1)}{2}$=2001000.
点评 本题考查了有理数的加法,解决本题的关键是明确等差数列和=(首项+末项)×项数÷2.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
13.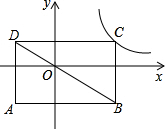 如图,在平面直角坐标系中,矩形ABCD的边平行于坐标轴,对角线BD经过坐标原点,点C在函数y=$\frac{k}{x}$(k>0,x>0)的图象上.若点A的坐标为(-3,-3),则k的值为( )
如图,在平面直角坐标系中,矩形ABCD的边平行于坐标轴,对角线BD经过坐标原点,点C在函数y=$\frac{k}{x}$(k>0,x>0)的图象上.若点A的坐标为(-3,-3),则k的值为( )
 如图,在平面直角坐标系中,矩形ABCD的边平行于坐标轴,对角线BD经过坐标原点,点C在函数y=$\frac{k}{x}$(k>0,x>0)的图象上.若点A的坐标为(-3,-3),则k的值为( )
如图,在平面直角坐标系中,矩形ABCD的边平行于坐标轴,对角线BD经过坐标原点,点C在函数y=$\frac{k}{x}$(k>0,x>0)的图象上.若点A的坐标为(-3,-3),则k的值为( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
11.将方程x2+8x+9=0配方后,原方程可变形为( )
| A. | (x+4)2=7 | B. | (x+4)2=25 | C. | (x+4)2=-9 | D. | (x+8)2=7 |
12.某工人若每小时生产38个零件,在规定时间内还有15个不能完成,若每小时生产42个零件,则可以超额完成5个,问:规定时间是多少?设规定时间为x小时,则可列方程为( )
| A. | 38x-15=42x+5 | B. | 38x+15=42x-5 | C. | 42x+38x=15+5 | D. | 42x-38x=15-5 |
 已知:如图,∠BOC=2∠AOC,OD平分∠AOB,且∠AOB=120°,求∠AOC和∠COD的度数.
已知:如图,∠BOC=2∠AOC,OD平分∠AOB,且∠AOB=120°,求∠AOC和∠COD的度数.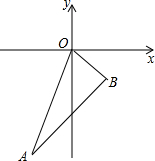 如图,直线OA的解析式为y=3x,点 A的横坐标是-1,OB=$\sqrt{2}$,OB与x轴所夹锐角是45°.
如图,直线OA的解析式为y=3x,点 A的横坐标是-1,OB=$\sqrt{2}$,OB与x轴所夹锐角是45°. 如图所示,已知数轴上两点A、B对应的数分别为-2、4,点P为数轴上一动点.
如图所示,已知数轴上两点A、B对应的数分别为-2、4,点P为数轴上一动点.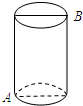 如图,圆柱体的高为12cm,底面周长为10cm,圆柱下底面A点除有一只蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是13cm.
如图,圆柱体的高为12cm,底面周长为10cm,圆柱下底面A点除有一只蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是13cm.