题目内容
17. 如图所示,已知数轴上两点A、B对应的数分别为-2、4,点P为数轴上一动点.
如图所示,已知数轴上两点A、B对应的数分别为-2、4,点P为数轴上一动点.(1)写出点A对应的数的倒数和绝对值;
(2)若点P到点A,点B的距离相等,求点P在数轴上对应的数;
(3)将点B向左移动7个单位长度,再向右移动2个单位长度,得到点C,在数轴上画出点C,并写出点C表示的是数.
分析 (1)根据倒数的定义和绝对值的性质可得点A对应的数的倒数和绝对值;
(2)根据中点坐标公式可得点P在数轴上对应的数;
(3)根据将点B向左移动7个单位长度,再向右移动2个单位长度,得到点C,可以得到点C表示的数,从而可以在数轴上表示出点C,并得到点C表示的数.
解答 解:(1)点A对应的数的倒数是-$\frac{1}{2}$,
点A对应的数的绝对值是2;
(2)(-2+4)÷2
=2÷2
=1.
故点P在数轴上对应的数是1;
(3)如图所示:点C表示的数是-1.
点评 本题考查数轴、倒数、绝对值,解题的关键是明确数轴的含义,利用数形结合的思想解答问题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
8.正确的算式是( )
| A. | (-1)2011=-2011 | B. | 2(-3)2=36 | C. | -3÷$\frac{1}{2}$×2=-3 | D. | $\frac{1}{2}$÷(-$\frac{1}{2}$)=-1 |
12.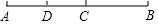 如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=10.5cm,那么BC的长为( )
如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=10.5cm,那么BC的长为( )
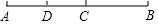 如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=10.5cm,那么BC的长为( )
如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=10.5cm,那么BC的长为( )| A. | A2.5cm | B. | 3cm | C. | 4.5cm | D. | 6cm |

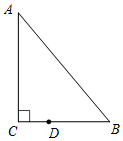 如图,Rt△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把线段BD 绕着点D逆时针旋转α(0<α<180)度后,如果点B恰好落在Rt△ABC的边上,那么α=70°或120°.
如图,Rt△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把线段BD 绕着点D逆时针旋转α(0<α<180)度后,如果点B恰好落在Rt△ABC的边上,那么α=70°或120°.