题目内容
11.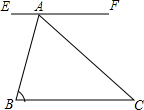 如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是( )
如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是( )| A. | 70° | B. | 60° | C. | 55° | D. | 50° |
分析 首先根据平行线的性质,可得∠EAB=∠B=50°,∠C=∠CAF,据此求出∠BAF的度数是多少,然后根据AC平分∠BAF,求出∠CAF的度数是多少,即可求出∠C的度数.
解答 解:∵EF∥BC,
∴∠EAB=∠B=70°,∠C=∠CAF,
∴∠BAF=180°-70°=110°,
又∵AC平分∠BAF,
∴∠CAF=110°÷2=55°,
∴∠C=55°.
故选:C.
点评 主要考查了平行线的性质:
①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.
定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.
③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.小明同学5次数学单元测试的平均成绩是90分,中位数是91分,众数是94分,则两次最低成绩之和是( )
| A. | 165分 | B. | 168分 | C. | 170分 | D. | 171分 |
3.如果单项式2anb2c是六次单项式,那么n的值取( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
 如图,已知△ABC中,AB=AC.
如图,已知△ABC中,AB=AC.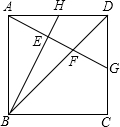 如图,正方形ABCD,H为AD中点,AG⊥BH分别交BH、BD、CD于E、F、G.
如图,正方形ABCD,H为AD中点,AG⊥BH分别交BH、BD、CD于E、F、G. 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,α),点B(2,n)是反比例函数图象上一点,连接OB.
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,α),点B(2,n)是反比例函数图象上一点,连接OB.