题目内容
13.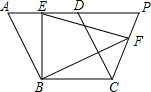 如图,在平行四边形ABCD,BE⊥AD于点E,且点E为AD中点,tanA=2,点P在AD的延长线上,作EF⊥CP于点F,连接BF.
如图,在平行四边形ABCD,BE⊥AD于点E,且点E为AD中点,tanA=2,点P在AD的延长线上,作EF⊥CP于点F,连接BF.(1)若BC=4,求CD的长;
(2)求证:CF=$\sqrt{2}$BF-EF.
分析 (1)在RT△求出AB,再利用平行四边形的性质即可解决问题.
(2)将△EBF绕点B顺时针旋转90°得到△BCM,只要证明①F、C、M共线,②△BFM是等腰直角三角形即可.
解答 (1)解: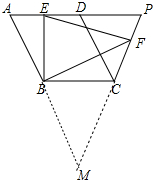 ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴AD∥CB,AD=BC=4,AB=CD
∵AE=ED=2,tanA=2,∠AEB=90°,
∴$\frac{EB}{AE}$=2,BE=4,
在RT△ABE中,∵AE=2,BE=4,
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
(2)证明:∵BC=BE,∠EBC=90°,
∴可以将△EBF绕点B顺时针旋转90°得到△BCM,
∵∠EBC+∠EFC=180°,
∴∠BEF+∠BCF=180°,
∵∠BEF=∠BCM
∴∠BCF+∠BCM=180°,
∴F、C、M共线,BF=BM,∠FBM=90°,
∴FM=$\sqrt{2}$BF,
∵EF=CM,
∴EF+CF=CM+CF=FM=$\sqrt{2}$FB.
∴CF=$\sqrt{2}$FB-EF.
点评 本题考查平行四边形的性质、勾股定理、三角函数的定义等知识,解题的关键是利用旋转法添加辅助线,构造全等三角形,属于中考常考题型.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
4.国务院总理李克强在第十二届全国人大第四次政府工作报告中指出,2015年我国国内生产总值达到了67.7万亿元,67.7万亿元用科学记数法表示为( )
| A. | 67.7×1012 | B. | 6.77×1013 | C. | 0.677×1014 | D. | 6.77×1014 |
8.下列说法正确的是( )
| A. | 相等的角是对顶角 | |
| B. | 同旁内角相等,两直线平行 | |
| C. | 直线外一点到这条直线的垂线段,叫做点到直线的距离 | |
| D. | 经过直线外一点,有且只有一条直线与这条直线平行 |
5.平面直角坐标系中,正六边形ABCDEF的起始位置如图1所示,边AB在x轴上,现将正六边形沿x轴正方向无滑动滚动,第一次滚动后,边BC落在x轴上(如图2);第二次滚动后,边CD落在x轴上,如此继续下去.则第2016次滚动后,落在x轴上的是( )


| A. | 边DE | B. | 边EF | C. | 边FA | D. | 边AB |
3.如果单项式2anb2c是六次单项式,那么n的值取( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
 如图,已知△ABC中,AB=AC.
如图,已知△ABC中,AB=AC.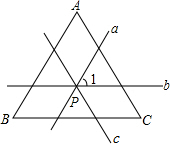 如图,P为△ABC内任意一点,过点P分别画a∥AB,b∥BC,c∥AC.那么只要再给出∠A、∠B、∠C三个角中哪一个角的度数,即可求得∠1的度数?试说明你的理由.
如图,P为△ABC内任意一点,过点P分别画a∥AB,b∥BC,c∥AC.那么只要再给出∠A、∠B、∠C三个角中哪一个角的度数,即可求得∠1的度数?试说明你的理由.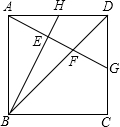 如图,正方形ABCD,H为AD中点,AG⊥BH分别交BH、BD、CD于E、F、G.
如图,正方形ABCD,H为AD中点,AG⊥BH分别交BH、BD、CD于E、F、G.