Question

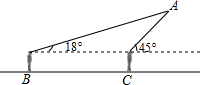如图，为了知道空中一静止的广告气球A的高度，小宇在B处测得气球A的仰角为18°，他向前走了20m到达C处后，再次测得气球A的仰角为45°，已知小宇的眼睛距地面1.6m，求此时气球A距地面的高度（结果精确到0.1m）．

Answer 1

考点：解直角三角形的应用-仰角俯角问题

专题：代数几何综合题

分析：作AD⊥BC于点D，交FG于点E，则△AGE是等腰直角三角形，设AE长是xm，在直角△AFE中，利用三角函数即可列方程求得AE的长，则AD即可求得．

解答：解：作AD⊥BC于点D，交FG于点E．
∵∠AGE=45°，
∴AE=GE，
在直角△AFE中，设AE长是xm，
则tan∠AFE=

AE

EF

，即tan18°=

x

x+20

，
解得：x≈9.6．
则ED=FB≈1.6．
∴AD=9.6+1.6=11.2m．
答：此时气球A距地面的高度是11.2m．

点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．