题目内容
 如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC=1,O为AC的中点,OE⊥OD交AB于点E.若AE=
如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC=1,O为AC的中点,OE⊥OD交AB于点E.若AE=| 3 |
| 4 |
考点:全等三角形的判定与性质,勾股定理,等腰直角三角形
专题:
分析:求出△DAO≌△EBO,推出OD=OE,AD=BE,求出AD=BE=
,由勾股定理得出DE2=DO2+OE2=AD2+AE2,求出即可.
| 1 |
| 4 |
解答:解:∵∠ABC=90°,O为AC的中点,
∴∠CAB=∠ACB=45°,∠ABO=45°,AO=BO=CO,∠AOB=90°,
∵OE⊥OD,
∴∠DOE=∠AOB=90°,
∴∠DOA=∠BOE=90°-∠AOE,
∵AD∥BC,
∴∠DAB=180°-∠ABC=90°,
∴∠DAO=90°-45°=45°,
∴∠DAO=∠OBE,
在△DAO和△EBO中
∴△DAO≌△EBO(ASA),
∴OD=OE,AD=BE,
∵AB=1,AE=
,
∴AD=BE=1-
=
,
在Rt△DAE和Rt△DOE中,由勾股定理得:DE2=DO2+OE2=AD2+AE2,
∴2DO2=(
)2+(
)2,
DO=
,
故答案为:
.
∴∠CAB=∠ACB=45°,∠ABO=45°,AO=BO=CO,∠AOB=90°,
∵OE⊥OD,
∴∠DOE=∠AOB=90°,
∴∠DOA=∠BOE=90°-∠AOE,
∵AD∥BC,
∴∠DAB=180°-∠ABC=90°,
∴∠DAO=90°-45°=45°,
∴∠DAO=∠OBE,

在△DAO和△EBO中
|
∴△DAO≌△EBO(ASA),
∴OD=OE,AD=BE,
∵AB=1,AE=
| 3 |
| 4 |
∴AD=BE=1-
| 3 |
| 4 |
| 1 |
| 4 |
在Rt△DAE和Rt△DOE中,由勾股定理得:DE2=DO2+OE2=AD2+AE2,
∴2DO2=(
| 1 |
| 4 |
| 3 |
| 4 |
DO=
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查了等腰直角三角形性质,勾股定理,全等三角形的性质和判定的应用,解此题的关键是求出OD=OE,AD=BE,题目比较好,难度适中.

练习册系列答案
相关题目
分式方程
=
的解为( )
| 1 |
| x-1 |
| 2 |
| x2-1 |
| A、1 | B、-1 | C、无解 | D、±1 |
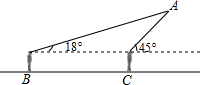 如图,为了知道空中一静止的广告气球A的高度,小宇在B处测得气球A的仰角为18°,他向前走了20m到达C处后,再次测得气球A的仰角为45°,已知小宇的眼睛距地面1.6m,求此时气球A距地面的高度(结果精确到0.1m).
如图,为了知道空中一静止的广告气球A的高度,小宇在B处测得气球A的仰角为18°,他向前走了20m到达C处后,再次测得气球A的仰角为45°,已知小宇的眼睛距地面1.6m,求此时气球A距地面的高度(结果精确到0.1m). 如图,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM的度数为
如图,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM的度数为 某校开展“好书伴我成长”的读书活动,为了解八年级450名学生的读书情况,随机调查了八年级50名学生本学期读书的册数,并将统计数据制成了扇形统计图,则该校八年级读书册数等于3册的约有
某校开展“好书伴我成长”的读书活动,为了解八年级450名学生的读书情况,随机调查了八年级50名学生本学期读书的册数,并将统计数据制成了扇形统计图,则该校八年级读书册数等于3册的约有 如图,已知∠1=∠2,∠3=73°,则∠4的度数为
如图,已知∠1=∠2,∠3=73°,则∠4的度数为