题目内容
15.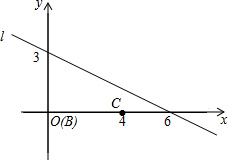 △ABC的两个顶点分别为B(0,0),C(4,0),顶点A在直线l:$y=-\frac{1}{2}x+3$上,
△ABC的两个顶点分别为B(0,0),C(4,0),顶点A在直线l:$y=-\frac{1}{2}x+3$上,(1)当△ABC是以BC为底的等腰三角形时,写出点A的坐标;
(2)当△ABC的面积为6时,求点A的坐标;
(3)在直线l上是否存在点A,使△ABC为Rt△?若存在,求出点A的坐标,若不存在说明理由.
分析 (1)作出线段BC的垂直平分线,与直线l交于点A,此时△ABC是以BC为底的等腰三角形,求出A坐标即可;
(2)由△ABC面积为6,根据BC的长,利用三角形面积公式求出A纵坐标,即可确定出A坐标;
(3)分三种情况考虑:∠ABC为直角;∠ACB为直角;∠BAC为直角,分别求出A坐标即可.
解答 解:(1)作出线段BC的垂直平分线,与直线l交于点A,连接BA,CA,此时△ABC是以BC为底的等腰三角形,如图1所示,
∵B(0,0),C(4,0),
∴A横坐标为x=2,
把x=2代入y=-$\frac{1}{2}$x+3,得:y=2,即A(2,2);
(2)∵△ABC面积为6,且BC=4,
∴$\frac{1}{2}$BC•|yA纵坐标|=6,即|yA纵坐标|=3,
把y=3代入y=-$\frac{1}{2}$x+3得:x=0;把y=-3代y=-$\frac{1}{2}$x+3得:x=12,
则A(0,3)或(12,-3);
(3)如图2所示,
分三种情况考虑:当∠A1BC=90°时,此时A1(0,3);
当∠BA2C=90°时,作A2D⊥x轴,设OA=m,A2D=-$\frac{1}{2}$m+3,DC=4-m,
由△A2BD∽△CA2D,得到A2D2=BD•DC,即(-$\frac{1}{2}$m+3)2=m(4-m),
解得:m=3.6或m=2,此时A2(3.6,1.2)或(2,2);
当∠A3CB=90°时,此时A3(4,1).
点评 此题属于一次函数综合题,涉及的知识有:坐标与图形性质,直角三角形的性质,相似三角形的判定与性质,以及一次函数的图象与性质,熟练掌握性质是解本题的关键.

练习册系列答案
相关题目
5.用代入法解方程组$\left\{\begin{array}{l}2x+3y=7\\ 5x-y=9\end{array}\right.$先消去未知数( )最简便.
| A. | x | B. | y | ||
| C. | 两个中的任何一个都一样 | D. | 无法确定 |
20.若a、b、c是△ABC的三边的长,则化简|a-b-c|-|b-c-a|+|a+b-c|=( )
| A. | a+b+c | B. | -a+3b-c | C. | a+b-c | D. | 2b-2c |
7.不等式组$\left\{\begin{array}{l}x>-2\\ x>a.\end{array}\right.$的解集是x>a,则a的取值范围是( )
| A. | a<-2 | B. | a=-2 | C. | a>-2 | D. | a≥-2 |
4.如图图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |