题目内容
13.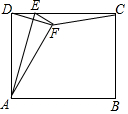 如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.
如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.
分析 分三种情况进行讨论:当DF=CF时,△DFC是等腰三角形;当DC=DF=6时,△DFC是等腰三角形;当DC=FC时,△DFC是等腰三角形,分别根据勾股定理、相似三角形的性质以及轴对称的性质进行计算求解.
解答 解:分三种情况:
①如图,当DF=CF时,△DFC是等腰三角形,
过F作FG⊥CD于G,交AB于H,则FH⊥AB,
∵DG=$\frac{1}{2}$CD=AH=3,AF=AD=5,
∴Rt△AFH中,HF=4,
∴GF=GH-FH=1,
设DE=FE=x,则EG=3-x,
∵Rt△EFG中,(3-x)2+12=x2,
解得x=$\frac{5}{3}$,
∴DE的长为$\frac{5}{3}$;
②如图,当DC=DF=6时,△DFC是等腰三角形,
由折叠可得,AE⊥DF,DO=$\frac{1}{2}$DF=3,
∴Rt△AOD中,AO=4,
∵∠ADE=90°,
∴∠ODE=∠OAD,
又∵∠DOE=∠AO90°,
∴△DOE∽△AOD,
∴$\frac{DE}{AD}$=$\frac{DO}{AO}$,即$\frac{DE}{5}$=$\frac{3}{4}$,
解得DE=$\frac{15}{4}$;
③如图,当DC=FC时,△DFC是等腰三角形,
∴点C在DF的垂直平分线上,
又∵AE垂直平分DF,
∴点E与点C重合,
∴DE=DC=6,
综上所述,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.
故答案为:$\frac{5}{3}$或$\frac{15}{4}$或6.
点评 本题主要考查了折叠问题,等腰三角形的性质,矩形的性质,相似三角形的判定与性质以及勾股定理的综合应用,解决问题的关键是依据△DFC是等腰三角形进行分类讨论,解题时注意方程思想以及分类思想的运用.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案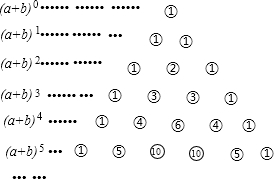
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
| A. | 2017 | B. | 2016 | C. | 191 | D. | 190 |
| A. | $\frac{1.2}{6}$+$\frac{1.2}{x}$=1 | B. | $\frac{1.2}{6}$+$\frac{1.2}{x}$=$\frac{1}{2}$ | C. | $\frac{1.2}{3}$+$\frac{1.2}{x}$=$\frac{1}{2}$ | D. | $\frac{1.2}{3}$+$\frac{1.2}{x}$=1 |
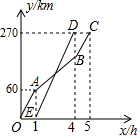 小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
小明家和邻居李叔叔家计划分别驾车去离家270km处的某景点旅游,商量好早上7:00出发,李叔叔因家中有事,8:00才出发,于是小明家便减慢了速度,为了追上小明家,李叔叔加快了行驶速度,结果比小明家先到,小明家知道后便以最初的速度全力向景区驶去,己知他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.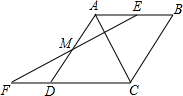 如图,点E在菱形ABCD边上,AE=1,过E作AC的垂线EF,交AD于点M,交CD的延长线于点F,DF=2,∠B=60°,点P是AC上的动点,则PM+PF的最小值3$\sqrt{3}$.
如图,点E在菱形ABCD边上,AE=1,过E作AC的垂线EF,交AD于点M,交CD的延长线于点F,DF=2,∠B=60°,点P是AC上的动点,则PM+PF的最小值3$\sqrt{3}$.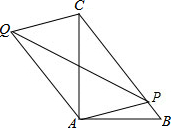 如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为$\frac{24}{5}$.
如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为$\frac{24}{5}$.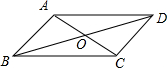 如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,
如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,