题目内容
3.已知关于x的一元二次方程kx2+x-2=0有两个不相等的实数根.(1)求实数k的取值范围;
(2)设方程两个实数根分别为x1,x2,且满足x12+x22+3x1•x2=3,求k的值.
分析 (1)根据一元二次方程的定义和判别式的意义得到k≠0且△=12-4k•(-2)>0,然后求出两个不等式的公共部分即可;
(2)根据根与系数的关系得到x1+x2=-$\frac{1}{k}$,x1x2=-$\frac{2}{k}$,再变形x12+x22+3x1•x2=3得到(x1+x2)2+x1•x2=3,所以(-$\frac{1}{k}$)2-$\frac{2}{k}$=3,然后解方程后利用(1)中的范围确定满足条件的k的值.
解答 解:(1)根据题意得k≠0且△=12-4k•(-2)>0,
解得k>-$\frac{1}{8}$且k≠0;
(2)根据题意得x1+x2=-$\frac{1}{k}$,x1x2=-$\frac{2}{k}$,
∵x12+x22+3x1•x2=3,
∴(x1+x2)2+x1•x2=3,
∴(-$\frac{1}{k}$)2-$\frac{2}{k}$=3,
整理得3k2+2k-1=0,解得k1=$\frac{1}{3}$,k2=-1,
∵k>-$\frac{1}{8}$且k≠0,
∴k=$\frac{1}{3}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.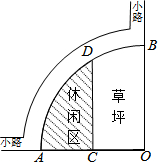 如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
 如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )| A. | $(6π-\frac{9}{2}\sqrt{3}){m^2}$ | B. | $(6π-9\sqrt{3}){m^2}$ | C. | $(π-\frac{9}{2}\sqrt{3}){m^2}$ | D. | $(10π-\frac{9}{2}\sqrt{3}){m^2}$ |
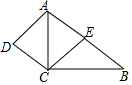 如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.
如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.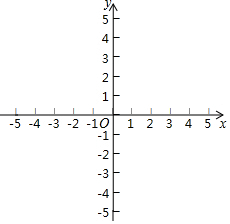 已知一次函数y1=k1x+b1的图象过点M(-1,6),Q(3,-2),一次函数y2=k2x+b2的图象过点N(-3,-6),P(3,6).
已知一次函数y1=k1x+b1的图象过点M(-1,6),Q(3,-2),一次函数y2=k2x+b2的图象过点N(-3,-6),P(3,6).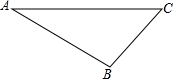 如图,已知△ABC
如图,已知△ABC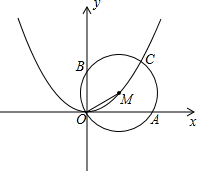 如图,M是抛物线y=ax2(a>0)上一点,以MO为半径画⊙M交x轴于点A(2,0),交y轴于点B,交抛物线于另一点C.若$\widehat{CA}$=$\widehat{CB}$,则a=$\frac{-1+\sqrt{5}}{2}$.
如图,M是抛物线y=ax2(a>0)上一点,以MO为半径画⊙M交x轴于点A(2,0),交y轴于点B,交抛物线于另一点C.若$\widehat{CA}$=$\widehat{CB}$,则a=$\frac{-1+\sqrt{5}}{2}$.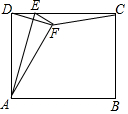 如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.
如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.