题目内容
18．
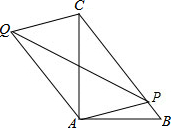如图，Rt△ABC中，∠BAC=90°，AB=6，AC=8，点P为BC上任意一点，连接PA，以PA、PC为邻边作平行四边形PAQC，连接PQ，则PQ的最小值为$\frac{24}{5}$．
分析 设PQ与AC交于点O，作OP′⊥BC于P′．首先求出OP′，当P与P′重合时，PQ的值最小，PQ的最小值=2OP′．
解答 解：设PQ与AC交于点O，作OP′⊥BC于P′．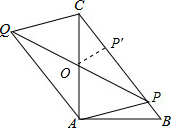
在Rt△ABC中，BC=$\sqrt{A{C}^{2}+A{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10，
∵∠OCP′=∠ACB，∠OP′C=∠CAB，
∴△COP′∽△CBA，
∴$\frac{CO}{CB}$=$\frac{OP′}{AB}$，
∴$\frac{4}{10}$=$\frac{OP′}{6}$，
∴OP′=$\frac{12}{5}$，
当P与P′重合时，PQ的值最小，PQ的最小值=2OP′=$\frac{24}{5}$．
故答案为$\frac{24}{5}$．
点评 本题考查平行四边形的性质．直角三角形的性质、勾股定理、垂线段最短等知识，解题的关键是学会添加常用辅助线，利用垂线段最短解决最值问题，属于中考常考题型．
练习册系列答案
相关题目
已知一次函数y1=k1x+b1的图象过点M（-1，6），Q（3，-2），一次函数y2=k2x+b2的图象过点N（-3，-6），P（3，6）．
9．已知函数y=ax2-2ax-1（a是常数，a≠0），下列结论正确的是（ ）
| A． | 当a=1时，函数图象过点（-1，1） | |
| B． | 当a=-2时，函数图象与x轴没有交点 | |
| C． | 若a＞0，则当x≥1时，y随x的增大而减小 | |
| D． | 不论a为何值，函数图象必经过（2，-1） |
6．通过调查，一段时间内，C、D两城生产化肥供给A、B两乡，其中A、B两乡需求总量y（吨）与化肥市场价格x（百元/吨）（3≤x≤8），存在下列关系：
C、D两城生产总量Z（吨）与化肥市价x（百元/吨）成正比例函数：Z=100x，已知C城生产总量为240吨，A乡需求量为200吨．如果需求量y与生产量Z相等，此时处于平衡状态．
（1）请通过描点画图，探究y与x之间的函数关系；
（2）某运输公司承担化肥运输任务，已知从C城运往A、B两乡运费分别为20元/t和15元/t；从D城运往A、B两乡费用分别未能25元/t和24元/t，当市场处于平衡状态时，如何调运可使总费用最少？并求出最小费用是多少元？
| x | 4 | 5 | 6 | 7 |
| y | 550 | 500 | 450 | 400 |
（1）请通过描点画图，探究y与x之间的函数关系；
（2）某运输公司承担化肥运输任务，已知从C城运往A、B两乡运费分别为20元/t和15元/t；从D城运往A、B两乡费用分别未能25元/t和24元/t，当市场处于平衡状态时，如何调运可使总费用最少？并求出最小费用是多少元？
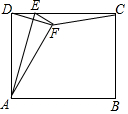如图矩形ABCD中，AD=5，AB=6，点E为DC上一个动点，把△ADE沿AE折叠，点D的对应点为F，当△DFC是等腰三角形时，DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6．
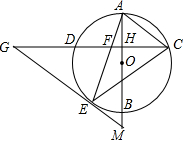如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．
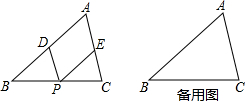在△ABC中，点P是BC上一动点（与B、C不重合），过点P作PD∥AC交AB于D．作PE∥AB交AC于E，则四边形AEPD是平行四边形．