题目内容
5.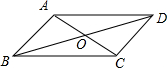 如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,
如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC:BD=1:2,(1)求AC的长;
(2)求△AOD的面积.
分析 (1)由题意,设OA=x.OB=2x,在Rt△AOB中,利用勾股定理即可求出x,即可解决问题.
(2)根据△AOD与△AOB的面积相等,即可解决问题.
解答 解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AC:BD=1:2,
∴OB=2OA,设OA=x.OB=2x,
在Rt△AOB中,∵AB2+OA2=OB2,
∴4+x2=4x2,
∴x=$\frac{2\sqrt{3}}{3}$,
∴AC=2OA=$\frac{4\sqrt{3}}{3}$.
(2)∵OB=OD,
∴S△AOD=S△AOB=$\frac{1}{2}$×2×$\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查平行四边形的性质、勾股定理等知识,解题的关键是学会利用参数,构建方程解决问题,属于中考常考题型.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
17.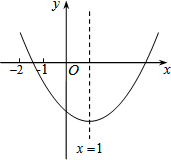 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①b2-4ac>0;②abc>0;③2a+b>0;④9a+3b+c<0;⑤8a+c>0.
其中,结论正确的个数是( )
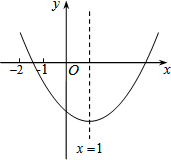 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③2a+b>0;④9a+3b+c<0;⑤8a+c>0.
其中,结论正确的个数是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
14.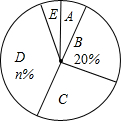 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
请你根据以上的信息,回答下列问题:
(1)被调查的学生中,最喜爱体育节目的有30人,这些学生数占被调查总人数的百分比为20%.
(2)被调查学生的总数为150人,统计表中m的值为45,统计图中n的值为36.
(3)在统计图中,E类所对应扇形圆心角的度数为21.6°.
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱新闻节目的学生数.
 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.| 类别 | A | B | C | D | E |
| 节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
| 人数 | 12 | 30 | m | 54 | 9 |
(1)被调查的学生中,最喜爱体育节目的有30人,这些学生数占被调查总人数的百分比为20%.
(2)被调查学生的总数为150人,统计表中m的值为45,统计图中n的值为36.
(3)在统计图中,E类所对应扇形圆心角的度数为21.6°.
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱新闻节目的学生数.
15. 如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
 如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )| A. | 传 | B. | 统 | C. | 文 | D. | 化 |
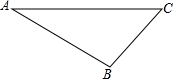 如图,已知△ABC
如图,已知△ABC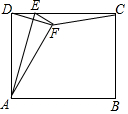 如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.
如图矩形ABCD中,AD=5,AB=6,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为F,当△DFC是等腰三角形时,DE的长为$\frac{5}{3}$或$\frac{15}{4}$或6.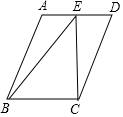 如图,面积为24的?ABCD中,BC=4,E是直线AD上一点,连接BE、CE,则sin∠BEC的最大值为$\frac{3}{5}$.
如图,面积为24的?ABCD中,BC=4,E是直线AD上一点,连接BE、CE,则sin∠BEC的最大值为$\frac{3}{5}$.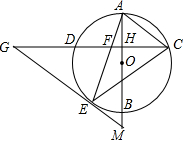 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.