题目内容
如图，在?ABCD中，E、F分别是AD、AB上的点，且BE=DF，BE交DF于P、交CD的延长线于Q，求证：CD：CQ=PD：PQ．考点：平行四边形的性质,相似三角形的判定与性质
专题：证明题
分析：首先根据平行四边形的性质得到两对相似三角形，列出两个比例式；然后运用比例的性质将所列的比例式转化、变形，即可解决问题．
解答：证明：∵四边形ABCD是平行四边形，∴BF∥DQ，DE∥BC，
∴△BFP∽△QDP，△DEQ∽△CBQ，
∴
=
①，
=
②；
由①得；
=
，即
=
，
∴
=
，而BE=DF，
∴
=
③，由②、③式知
=
，
即CD：CQ=PD：PQ．
∴△BFP∽△QDP，△DEQ∽△CBQ，
∴
| PD |
| PF |
| PQ |
| PB |
| CD |
| CQ |
| BE |
| BQ |
由①得；
| PD |
| PD+PF |
| PQ |
| PQ+PB |
| PD |
| DF |
| PQ |
| BQ |
∴
| PD |
| PQ |
| DF |
| DQ |
∴
| PD |
| PQ |
| BE |
| BQ |
| CD |
| CQ |
| PD |
| PQ |
即CD：CQ=PD：PQ．
点评：该题主要考查了平行四边形的性质、相似三角形的判定及其应用等问题；解题的关键是灵活运用比例的性质将所得的比例式变形、转化．
练习册系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
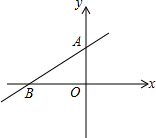已知一次函数y=（a-1）x+2（a-1）（a≠1）的图象如图所示，已知3OA=2OB，求一次函数的解析式．
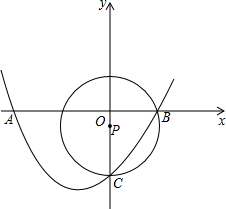已知：如图，抛物线y=ax2+bx+c（a≠0）经过X轴上的两点A（x1，0）、B（x2，0）和y轴上的点C（0，-1.5），⊙P的圆心P在y轴上，且经过B、C两点，若b=