��Ŀ����
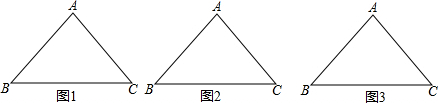
3����ͼ����Rt��ABC�У���ACB=90�㣬AC=6��BC=12��D��E�ֱ�Ϊ��AB��AC���е㣬����DE����P�ӵ�A������������AE-ED�˶�������Dֹͣ����P������AE-ED����ÿ��1����λ���ٶ��˶�������P��PQ��BC�ڵ�Q����PQΪ����PQ�Ҳ���������PQMN��ʹ��M�����߶�BC�ϣ����P���˶�ʱ��Ϊt�루t��0������1����������PQMN�Ķ���N����AB����ʱ����t��ֵ��
��2������BE����������PQMN���BED�ص�����ͼ�ε����ΪS����ֱ��д����3��t��9ʱ��S��t֮��ĺ�����ϵʽ����Ӧ���Ա���t��ȡֵ��Χ��
��3����������PQMN�Ķ���P�˶������E�غ�ʱ����������PQMN�Ƶ�Q��ʱ����ת60���������P1QM1N1������ֱ��DE��ֱ��AC���Ƿ���ڵ�G�͵�H��ʹ��GHP1�ǵ���ֱ�������Σ������ڣ������EG�ij����������ڣ���˵�����ɣ�����ͼ������̽������

���� ��1�����������Σ��ٵ���P��AE��ʱ����ͼ1�У��ɡ�APN�ס�ACB���Խ�����⣬�ڵ���P��ED��ʱ��PN=3����ͼ2�����AE+EP���ɡ�
��2������ͼ3�У���3��t��6ʱ���ص�����ͼ��Ϊ�ı���PGKN����ͼ4�У�����ͼ4�У���6��t��9���ص������������PGKHD���ֱ�������ɣ�
��3���������������ۼ��ɢٵ���P1GH=90�㣬�ڵ���P1HG=90�㣬�۵���GP1H=90��ʱ��
��� �⣺��1���ٵ���P��AE��ʱ����ͼ1�У�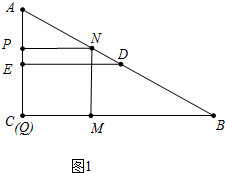
��PN��BC��
���APN�ס�ACB��
��$\frac{AP}{AC}$=$\frac{PN}{BC}$��
��$\frac{t}{6}$=$\frac{6-t}{12}$��
��t=2��
�ڵ���P��ED��ʱ��PN=3����ͼ2��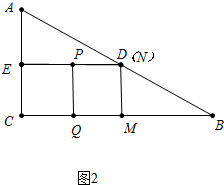
��AE+EP=3+��6-3��=6��
��t=6��
���Ͽɵ�t��ֵΪ2��6ʱ��������PQMN�Ķ���N����AB���ϣ�
��2����ͼ3�У���3��t��6ʱ���ص�����ͼ��Ϊ�ı���PGKN��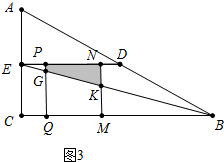
��GQ��EC��
��$\frac{GQ}{EC}$=$\frac{BQ}{BC}$��
��$\frac{GQ}{3}$=$\frac{15-t}{12}$��
��QG=$\frac{1}{4}$��15-t����PG=3-GQ=$\frac{t-3}{4}$��ͬ����֪NK=$\frac{t}{4}$��
��S=$\frac{1}{2}$[$\frac{1}{4}$��t-3��+$\frac{1}{4}$t]•3=$\frac{3}{4}$t-$\frac{9}{8}$��
��ͼ4�У���6��t��9���ص������������PGKHD��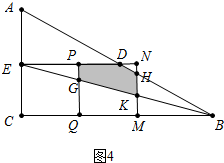
S=S�ı���PGHN-S��DNH=-$\frac{1}{4}t$2+$\frac{15}{4}$t-$\frac{81}{8}$��
����������S=$\left\{\begin{array}{l}{\frac{3}{4}t-\frac{9}{8}}&{��3��t��6��}\\{-\frac{1}{4}{t}^{2}+\frac{15}{4}t-\frac{81}{8}}&{��6��t��9��}\end{array}\right.$��
��3�����ڣ��������£�
��P1��P1S��AC��S��P1R��DE��R��
�ߡ�P1QS=60�㣬P1Q=3��
��P1S=RE=$\frac{3\sqrt{3}}{2}$��QS=$\frac{3}{2}$��
��P1R=SE=$\frac{3}{2}$��8��
�ٵ���P1GH=90��ʱ����ͼ5�У�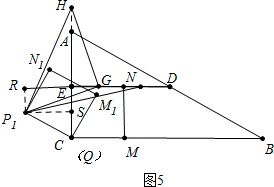

��֤��P1RG�ա�GEH��
��EG=P1R=$\frac{3}{2}$����ͼ6�У�ͬ���ɵ�EG=P1R=$\frac{3}{2}$��
�ڵ���P1HG=90��ʱ����ͼ7�У�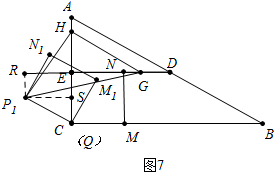
��֤��P1SH�ա�HEG��
��EH=P1S=$\frac{3\sqrt{3}}{2}$��EG=SH��
��EG=EH+SE=$\frac{3\sqrt{3}}{2}$+$\frac{3}{2}$��
����ͼ8�У�EG=EH-SE=$\frac{3\sqrt{3}}{2}$-$\frac{3}{2}$��
�۵���GP1H=90��ʱ��
��P1S��P1R�����P1SH���P1RG������ȫ�ȣ�
��P1H��P1G���������
���ϣ�EG�ij�Ϊ$\frac{3}{2}$��$\frac{3\sqrt{3}}{2}$+$\frac{3}{2}$��$\frac{3\sqrt{3}}{2}$-$\frac{3}{2}$��
���� ���⿼���������ۺ��⡢�����ε����ʡ�����ֱ�������ε����ʡ�ȫ�������ε��ж������ʡ�ƽ���ߵ����ʵ�֪ʶ������Ĺؼ���ѧ����ȷ����ͼ�Σ�ѧ�����÷ָ�������ѧ���������ע�ⲻ��©�⣬�����п�ѹ���⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | x��2 | B�� | x��-2 | C�� | -2��x��2 | D�� | x��-2�� x��2 |
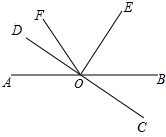 ��ͼ��ֱ��AB��CD�ཻ�ڵ�O����AOD=20�㣬��DOF����FOB=1��7������OEƽ�֡�BOF�����EOC=90�㣮
��ͼ��ֱ��AB��CD�ཻ�ڵ�O����AOD=20�㣬��DOF����FOB=1��7������OEƽ�֡�BOF�����EOC=90�㣮