Question

8．图1、图2分别是7×6的正方形网格，网格中每个小正方形的边长均为1，点A、B、C均在格点上（小正方形的顶点叫做格点）． 
（1）在图1中的格点上确定点D，并画出以A、B、C、D为顶点的四边形，使其既是轴对称图形又是中心对称图形（画一个即可）
（2）在图2中的格点上确定点E，并画出以A、B、C、E为顶点的四边形，使其为轴对称图形但不是中心对称图形（画一个即可）

Answer 1

分析 （1）可判定∠BAC=90°，分别过B作BD∥AC，过C作CD∥AB，四边形ABDC即为所求；
（2）作以AE、BC为底的等腰梯形即可．

解答 解：
（1）由图形可计算得出AB=$\sqrt{5}$，AC=4$\sqrt{5}$，BC=5，
满足AB²+AC²=BC²，
∴∠BAC=90°，
如图1，分别过B作BD∥AC，过C作CD∥AB，则四边形ABDC为矩形，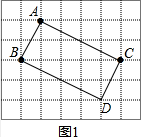

∴四边形ABDC既是轴对称图形又是中收对称图形；
（2）如图2，过A作AE∥BC，且使AE=3，则四边形ABCE为等腰梯形，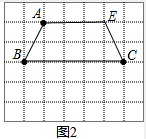

∴四边形ABCE是轴对称图形，但不是中心对称的图形．

点评 本题主要考查轴对称图形和中心对称图形的判定，掌握常见图形的对称性是解题的关键．