题目内容
13. 点D在等边三角形△ABC的边BC上,将△ABD绕点A旋转,使得旋转后点B的对应点为点C.
点D在等边三角形△ABC的边BC上,将△ABD绕点A旋转,使得旋转后点B的对应点为点C.(1)在图1中画出旋转后的图形.
(2)小颖是这样做的:如图2,过点C画BA的平行线L,在L上取CE=BD,连接AE,则△ACE即为旋转后的图形.小颖这样做对吗?请你说说理由.
分析 (1)直接利用旋转的性质得出对应点位置进而得出答案;
(2)直接利用等边三角形的性质结合全等三角形的判定方法进而得出答案.
解答 解:(1)如图1所示:△ACD′即为所求;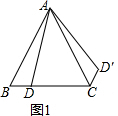
(2)小颖这样做对,
理由:如图2,∵△ABC是等边三角形,
∴AB=AC,∠B=∠ACB=60°,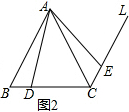
∵AB∥直线L,
∴∠B+∠BCE=180°,
∴∠ACE=60°,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠ACE}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴△ACE即为旋转后的图形.
点评 此题主要考查了旋转变换以及全等三角形的判定,正确应用等边三角形的性质是解题关键.

练习册系列答案
相关题目
4.在△ABC和△A′B′C′中,已知∠B=∠B′,BC=B′C′,下面判断中的错误是( )
| A. | 若添加条件AB=A′B′,则△ABC≌△A′B′C′ | |
| B. | 若添加条件AC=A′C′,则△ABC≌△A′B′C′ | |
| C. | 若添加条件∠C=∠C′,则△ABC≌△A′B′C′ | |
| D. | 若添加条件∠A=∠A′,则△ABC≌△A′B′C′ |
5.下列事件中,是确定事件的是( )
| A. | 度量三角形的内角和,结果是360° | B. | 买一张电影票,座位号是奇数 | ||
| C. | 打开电视机,它正在播放花样滑冰 | D. | 明天晚上会看到月亮 |
2.为了解某小区居民每月用水情况,随机抽查了该小区10户家庭的用水量,结果如表:
则这10户家庭的月平均用水量是14吨.
| 月用水量/吨 | 10 | 13 | 14 | 17 | 18 |
| 户数 | 2 | 2 | 3 | 2 | 1 |
2.不能判定两个三角形全等的条件是( )
| A. | 三条边对应相等 | B. | 两角及一边对应相等 | ||
| C. | 两边及夹角对应相等 | D. | 两边及一边的对角相等 |

 如图,Rt△ABC的直角边AC在x轴上,顶点A,B的坐标分别为A(10,0),B(6,8),直线y=kx分别交BC、AB与点M、N.
如图,Rt△ABC的直角边AC在x轴上,顶点A,B的坐标分别为A(10,0),B(6,8),直线y=kx分别交BC、AB与点M、N.