题目内容
18. 如图,Rt△ABC的直角边AC在x轴上,顶点A,B的坐标分别为A(10,0),B(6,8),直线y=kx分别交BC、AB与点M、N.
如图,Rt△ABC的直角边AC在x轴上,顶点A,B的坐标分别为A(10,0),B(6,8),直线y=kx分别交BC、AB与点M、N.(1)求出直线AB的函数解析式;
(2)若直线y=kx交线段AB与点N,当AN=2$\sqrt{5}$时,请说明直线y=kx垂直线段AB;
(3)在(2)的条件下,求MC的长.
分析 (1)设直线AB的函数解析式为y=mx+n,结合点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)过点N作NE⊥x轴于点E,由平行线的性质找出比例关系$\frac{NE}{BC}=\frac{EA}{CA}=\frac{AN}{AB}$,从而找出NE的长度,通过解直角三角形找出ON的长度,再根据勾股定理逆定理ON2+NA2=OA2,即可得出结论;
(3)由BC∥NE根据平行线的性质即可得出$\frac{MC}{NE}=\frac{OC}{OE}$,代入数据即可得出结论.
解答 解:(1)设直线AB的函数解析式为y=mx+n,
将点A(10,0)、B(6,8)代入y=mx+n中,
得:$\left\{\begin{array}{l}{0=10m+n}\\{8=6m+n}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-2}\\{n=20}\end{array}\right.$,
∴直线AB的函数解析式为y=-2x+20.
(2)过点N作NE⊥x轴于点E,如图1所示.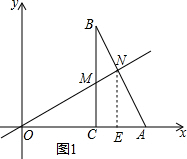
∵∠ACB=90°,NE⊥x轴,
∴BC∥NE,
∴$\frac{NE}{BC}=\frac{EA}{CA}=\frac{AN}{AB}$.
∵点A(10,0),B(6,8),
∴AB=4$\sqrt{5}$,BC=8,AC=4,
∴NE=4,AE=2,
在Rt△OEN中,NE=4,OE=OA-AE=8,
∴ON=4$\sqrt{5}$,
∴ON2+NA2=OA2,
∴直线y=kx垂直线段AB.
(3)∵BC∥NE,
∴$\frac{MC}{NE}=\frac{OC}{OE}$.
∵OC=OA-AC=6,OE=8,NE=4,
∴MC=3.
点评 本题考查了待定系数法求函数解析式、平行线的性质以及勾股定理,解题的关键是:(1)利用待定系数法求出函数解析式;(2)利用勾股定理来证垂直;(3)根据平行线的性质求出MC的长.本题属于中档题,难度不大,解决该题型题目时,根据平行线分线段成比例来解决问题是关键.

| A. | 长江某段水域的水污染情况的调查 | B. | 你校数学教师的年龄状况的调查 | ||
| C. | 各厂家生产的电池使用寿命的调查 | D. | 我市居民环保意识的调查 |
| A. | 0或1 | B. | 1或-1 | C. | 0或±1 | D. | 0 |
 如图,已知∠AOB=120°,OA⊥OC,BO⊥OD,则∠COD=60度.
如图,已知∠AOB=120°,OA⊥OC,BO⊥OD,则∠COD=60度. 如图,在直角坐标系中,点A(0,6)、B(8,0),动点P从点A出发在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B出发在线段上以每秒2个单位长度的速度向点A移动,其中一点到达终点时另一点也随之停止,设点P、Q移动的时间为t秒.
如图,在直角坐标系中,点A(0,6)、B(8,0),动点P从点A出发在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B出发在线段上以每秒2个单位长度的速度向点A移动,其中一点到达终点时另一点也随之停止,设点P、Q移动的时间为t秒. 点D在等边三角形△ABC的边BC上,将△ABD绕点A旋转,使得旋转后点B的对应点为点C.
点D在等边三角形△ABC的边BC上,将△ABD绕点A旋转,使得旋转后点B的对应点为点C.
 如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.
如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.