题目内容
7.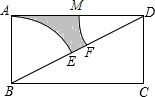 如图,已知矩形ABCD中,AB=8,BC=5π.分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为4π.
如图,已知矩形ABCD中,AB=8,BC=5π.分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为4π.
分析 由题意和图形可得,阴影部分的面积等于△ABD的面积与扇形ABE和扇形DMF的差,而两个扇形的半径相等,所对的圆心角的和等于90°,从而可以把两个扇形合在一起正好是四分之一个圆,然后计算出它们的面积作差,本题得以解决.
解答 解:∵在矩形ABCD中,AB=8,BC=5π,
∴∠BAC=90°,∠ABD+∠ADB=90°,BC=AD=5π,
∴${S}_{△ABD}=\frac{AB×AD}{2}=\frac{8×5π}{2}=20π$,
∵以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,
∴S扇形ABE+S扇形DMF=$\frac{90°}{360°}×π×{8}^{2}=16π$,
∴S阴影AEMF=S△ABD-S扇形ABE-S扇形DMF=20π-16π=4π,
故答案为:4π.
点评 本题考查扇形面积的计算,解题的关键是明确题意,利用数形结合和转化的数学思想,来解答本题.

练习册系列答案
相关题目
14.满足-$\sqrt{5}$<x<$\sqrt{3}$的整数x是( )
| A. | -2,1,0,1,2 | B. | -1,0,1,2,3 | C. | -2,-1,0,1 | D. | -1,0,1,2 |
15. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )
①ac>0.②当x>1时,y随x的增大而减小.③b-2a=0.④b2-4ac>0.⑤x=3是关于x的方程ax2+bx+c=0(a≠0)的一个根.
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )①ac>0.②当x>1时,y随x的增大而减小.③b-2a=0.④b2-4ac>0.⑤x=3是关于x的方程ax2+bx+c=0(a≠0)的一个根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.用配方法解方程x2+4x-3=0,配方后的方程可以是( )
| A. | (x-2)2=1 | B. | (x+2)2=1 | C. | (x-2)2=7 | D. | (x+2)2=7 |
16. y=kx+b的图象如图,当y<0时,自变量x的范围是( )
y=kx+b的图象如图,当y<0时,自变量x的范围是( )
 y=kx+b的图象如图,当y<0时,自变量x的范围是( )
y=kx+b的图象如图,当y<0时,自变量x的范围是( )| A. | x<-2 | B. | x>0 | C. | x<0 | D. | x>2 |
17.已知m-n=-1,则(m-n)2+3(n-m)+2的值是( )
| A. | 6 | B. | 4 | C. | 0 | D. | 2 |

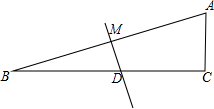 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,求AC的长.
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,求AC的长.