题目内容
5.设m,n为正整数,且m<$\sqrt{65}$+1<n,则m+n=19.分析 首先$\sqrt{64}$<$\sqrt{65}$$<\sqrt{81}$,得出9<$\sqrt{65}$+1<10,从而求得m=9,n=10,即可求得m+n的值.
解答 解:∵8<$\sqrt{65}$<9,
∴9<$\sqrt{65}$+1<10,
∴m=9,n=10,
∴m+n=19.
故答案为19.
点评 此题主要考查了估算无理数,得出8<$\sqrt{65}$<9是解题关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
16.用配方法解方程x2-2x-6=0时,原方程应变形为( )
| A. | (x+1)2=7 | B. | (x-1)2=7 | C. | (x+2)2=10 | D. | (x-2)2=10 |
14.满足-$\sqrt{5}$<x<$\sqrt{3}$的整数x是( )
| A. | -2,1,0,1,2 | B. | -1,0,1,2,3 | C. | -2,-1,0,1 | D. | -1,0,1,2 |
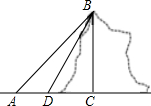 如图,小明在A处用测角仪观测一座山的山顶B的仰角为45°,然后他前进了50米到达D处,观测B处的仰角为60°,求小山的高度BC(结果要求精确到1米,参考数据:$\sqrt{3}$≈1.7)
如图,小明在A处用测角仪观测一座山的山顶B的仰角为45°,然后他前进了50米到达D处,观测B处的仰角为60°,求小山的高度BC(结果要求精确到1米,参考数据:$\sqrt{3}$≈1.7)