题目内容
20．（1）式子$\frac{a}{bc}$+$\frac{b}{ca}$+$\frac{c}{ab}$的值能否为0？为什么？（2）式子$\frac{a-b}{（b-c）（c-a）}$+$\frac{b-c}{（a-b）（c-a）}$+$\frac{c-a}{（a-b）（b-c）}$的值能否为0？为什么？
分析 （1）原式通分并利用同分母分式的加减法则计算得到最简结果，判断即可；
（2）原式通分并利用同分母分式的加减法则计算得到最简结果，判断即可．
解答 解：（1）原式=$\frac{{a}^{2}+{b}^{2}+{c}^{2}}{abc}$，不能为0，若原式为0，只能a=b=c=0，没有意义；
（2）原式=$\frac{（a-b）^{2}+（b-c）^{2}+（c-a）^{2}}{（a-b）（b-c）（c-a）}$，不能为0，若原式为0，只能a=b=c，没有意义．
点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
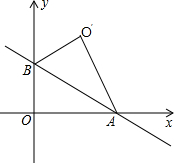如图，直线y=-$\frac{\sqrt{3}}{3}$x+2与x轴、y轴分别交于A、B两点，把△AOB沿直线AB翻折后得到△AO′B，则点O′的坐标是（$\sqrt{3}$，3）．
已知：如图，∠AOB=30°，∠DOB是直角，且∠COD=45°，求∠AOC的度数．
15．
如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹．反弹时反射角等于入射角，当点P第2016次碰到矩形的边时，点P的坐标为（ ）
如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹．反弹时反射角等于入射角，当点P第2016次碰到矩形的边时，点P的坐标为（ ）| A． | （0，3） | B． | （5，0） | C． | （7，4） | D． | （8，3） |
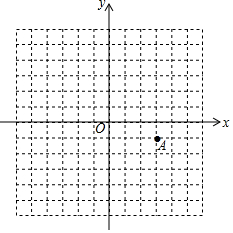如图，在网格中有点A（3，-1）．