题目内容
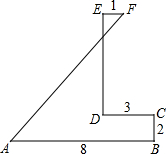小明在电脑上玩“荒岛去寻宝”游戏．寻宝人从点A登陆，先向正东走8cm，再向正北走，走了2cm，遇上礁石，只好改道向正西走，走了3cm后，再向正北走6cm，再向正东走1cm，找到了藏宝地点F．小明很快画出了寻宝图（如图），你知道宝藏地点离寻宝人登陆点的距离是多少厘米？考点：勾股定理的应用
专题：
分析：构造直角三角形利用勾股定理求得线段AE的长即可确定本题的答案．
解答：
解：作FG⊥AB于点G，
由题意得：FG=ED+BC=6+2=8cm，AG=8-2=6cm，
由勾股定理得：AF=
=
=10cm，
所以宝藏地点离寻宝人登陆点的距离是10cm．
解：作FG⊥AB于点G，由题意得：FG=ED+BC=6+2=8cm，AG=8-2=6cm，
由勾股定理得：AF=
| AG2+FG2 |
| 62+82 |
所以宝藏地点离寻宝人登陆点的距离是10cm．
点评：本题考查了勾股定理的应用，解题的关键是从实际问题中抽象出直角三角形，难度不大．
练习册系列答案
相关题目
分式方程
-1=
去分母后的结果正确的是（ ）
| x |
| x-2 |
| 1 |
| x2-4 |
| A、x2-4-1=1 |
| B、x2+2x-（x2-4）=1 |
| C、x+2-x2-4=1 |
| D、x+2-1=1 |
点A为反比例函数图象上一点，它到原点的距离为5，则x轴的距离为3，若点A第二象限内，则这个函数的解析式为（ ）
A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|