题目内容
探究与发现:你能很快算出10052吗?
这是一类个位数为5的自然数计算平方的问题,我们利用“从特殊到一般”的方法,计算以下简单情况,然后从中探索规律:
(1)计算:152= ;252= ;352= ;
(2)若个位数为5的自然数记作10n+5(其中n为自然数),从第(1)题的计算结果归纳猜想,发现(10n+5)2= ;
(3)根据上面规律,计算10052= .
这是一类个位数为5的自然数计算平方的问题,我们利用“从特殊到一般”的方法,计算以下简单情况,然后从中探索规律:
(1)计算:152=
(2)若个位数为5的自然数记作10n+5(其中n为自然数),从第(1)题的计算结果归纳猜想,发现(10n+5)2=
(3)根据上面规律,计算10052=
考点:规律型:数字的变化类
专题:
分析:根据题目给出的计算过程可得规律:第n个数可以表示为100×n×(n+1)+25,据此填空即可.
解答:解:根据规律,第n个数可以表示为100×n×(n+1)+25,
则:(1)152=100×1×(1+1)+25=225,252=100×2×(2+1)+25=625,352=100×3×(3+1)+25=1225;
(2)(10n+5)2=100×n×(n+1)+25;
(3)10052=(100×10+5)2=100×100×(100+1)+25=1010025.
故答案为:100×1×(1+1)+25=225,100×2×(2+1)+25=625,100×3×(3+1)+25=1225;100×n×(n+1)+25;1010025.
则:(1)152=100×1×(1+1)+25=225,252=100×2×(2+1)+25=625,352=100×3×(3+1)+25=1225;
(2)(10n+5)2=100×n×(n+1)+25;
(3)10052=(100×10+5)2=100×100×(100+1)+25=1010025.
故答案为:100×1×(1+1)+25=225,100×2×(2+1)+25=625,100×3×(3+1)+25=1225;100×n×(n+1)+25;1010025.
点评:此题考查了完全平方数的计算技巧,同时考查了规律的探索问题,可以激发同学们的探索意识,激发学习兴趣.

练习册系列答案
相关题目


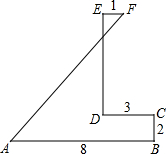 小明在电脑上玩“荒岛去寻宝”游戏.寻宝人从点A登陆,先向正东走8cm,再向正北走,走了2cm,遇上礁石,只好改道向正西走,走了3cm后,再向正北走6cm,再向正东走1cm,找到了藏宝地点F.小明很快画出了寻宝图(如图),你知道宝藏地点离寻宝人登陆点的距离是多少厘米?
小明在电脑上玩“荒岛去寻宝”游戏.寻宝人从点A登陆,先向正东走8cm,再向正北走,走了2cm,遇上礁石,只好改道向正西走,走了3cm后,再向正北走6cm,再向正东走1cm,找到了藏宝地点F.小明很快画出了寻宝图(如图),你知道宝藏地点离寻宝人登陆点的距离是多少厘米?