题目内容
点A为反比例函数图象上一点，它到原点的距离为5，则x轴的距离为3，若点A第二象限内，则这个函数的解析式为（ ）
A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
考点：待定系数法求反比例函数解析式
专题：
分析：先设A点坐标为（x，y），根据A点到x轴的距离为3，得出y=±3，根据A点到原点的距离为5，得出x=±4，从而根据点A的位置确定点A的坐标，再设这个反比例函数的解析式为y=
，再把已知点A的坐标代入可求出k值，即得到反比例函数的解析式．
| k |
| x |
解答：解：设A点坐标为（x，y）．
∵A点到x轴的距离为3，∴|y|=3，y=±3．
∵A点到原点的距离为5，∴x2+y2=52，
解得x=±4，
∵点A在第二象限，
∴x=-4，
∴点A的坐标为（-4，3），
设反比例函数的解析式为y=
，
∴k=-4×3=-12，
∴反比例函数的解析式为y=-
，
故选B．
∵A点到x轴的距离为3，∴|y|=3，y=±3．
∵A点到原点的距离为5，∴x2+y2=52，
解得x=±4，
∵点A在第二象限，
∴x=-4，
∴点A的坐标为（-4，3），
设反比例函数的解析式为y=
| k |
| x |
∴k=-4×3=-12，
∴反比例函数的解析式为y=-
| 12 |
| x |
故选B．
点评：本题考查的是反比例函数图象上点的坐标特征及用待定系数法求反比例函数的解析式，是中学阶段的重点内容．
练习册系列答案
相关题目
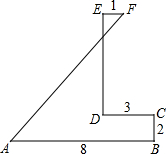小明在电脑上玩“荒岛去寻宝”游戏．寻宝人从点A登陆，先向正东走8cm，再向正北走，走了2cm，遇上礁石，只好改道向正西走，走了3cm后，再向正北走6cm，再向正东走1cm，找到了藏宝地点F．小明很快画出了寻宝图（如图），你知道宝藏地点离寻宝人登陆点的距离是多少厘米？