题目内容
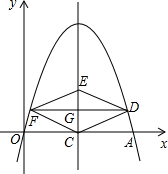 如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点.
如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点.(1)求这条抛物线的解析式.
(2)当点E落在抛物线顶点上时,求DF的长.
(3)当四边形CDEF是正方形时,求点E的坐标.
考点:二次函数综合题
专题:
分析:(1)把A点的坐标代入抛物线的解析式,求出b的值即可得到抛物线的解析式;
(2)由(1)可知抛物线的顶点坐标,因为G是EC中点,由此可求出G的纵坐标,代入抛物线的解析式可求出F和D的横坐标,进而可求出DF的长;
(3)四边形CDEF是正方形时可设设E(2,2m),则F(2-m,m),把F点的坐标代入解析式即可求出m的值,进而可求出点E的坐标.
(2)由(1)可知抛物线的顶点坐标,因为G是EC中点,由此可求出G的纵坐标,代入抛物线的解析式可求出F和D的横坐标,进而可求出DF的长;
(3)四边形CDEF是正方形时可设设E(2,2m),则F(2-m,m),把F点的坐标代入解析式即可求出m的值,进而可求出点E的坐标.
解答:解:(1)把(4,0)代入y=-x2+bx中,得b=4.
∴这条抛物线的解析式为y=-x2+4x.
(2)由(1)可知抛物线的顶点坐标为(2,4).
∵G是EC的中点,
∴当y=2时,-x2+4x=2.
∴x1=2-
,x2=2+
,.
∴DF=2+
-(2-
)=2
.
(3)设E(2,2m),则F(2-m,m).
∵点F在抛物线上,
∴m=-(2-m)2+4(2-m).
∴m=
,2m=-1±
.
∴E1(2,-1+
),E2=(2,-1-
).
∴这条抛物线的解析式为y=-x2+4x.
(2)由(1)可知抛物线的顶点坐标为(2,4).
∵G是EC的中点,
∴当y=2时,-x2+4x=2.
∴x1=2-
| 2 |
| 2 |
∴DF=2+
| 2 |
| 2 |
| 2 |
(3)设E(2,2m),则F(2-m,m).
∵点F在抛物线上,
∴m=-(2-m)2+4(2-m).
∴m=
-1±
| ||
| 2 |
| 17 |
∴E1(2,-1+
| 17 |
| 17 |
点评:本题考查了用待定系数法求二次函数的解析式、解一元二次方程以及正方形的性质,题目的综合性较强,难度中等.

练习册系列答案
相关题目
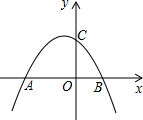 如图,抛物线y=-
如图,抛物线y=-
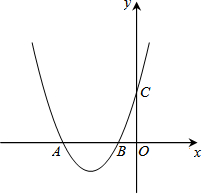 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(ac≠0)与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C.若线段OA、OB、OC的长满足OC2=OA•OB,则这样的抛物线称为“黄金”抛物线.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(ac≠0)与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C.若线段OA、OB、OC的长满足OC2=OA•OB,则这样的抛物线称为“黄金”抛物线.