题目内容
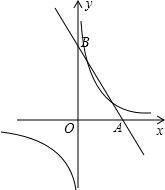 已知,如图,函数y=
已知,如图,函数y=| 6 |
| x |
(1)直接写出A、B两点的坐标:A
(2)观察图象,直接写出不等式
| 6 |
| x |
(3)点P是坐标轴上的动点,当AP+BP取得最小值时,求点P的坐标.
考点:反比例函数与一次函数的交点问题,轴对称-最短路线问题
专题:
分析:(1)一次函数与反比例函数组成方程组即可求得交点坐标;
(2)根据反比例函数图象在一次函数图象上方的部分,是反比例函数值大于一次函数值,可得答案;
(3)分两种情况:①点P在x轴上,作点A关于x轴的对称点A′(3,-2),连结A′B交x轴于点P,利用轴对称得出AP+BP的最小值为线段A′B,进而利用待定系数法求出解析式,即可得出P点坐标;②点P在y轴上,作点B关于y轴的对称点B′(-1,6),连结AB′交y轴于点P,利用轴对称得出AP+BP的最小值为线段AB′,进而利用待定系数法求出解析式,即可得出P点坐标.
(2)根据反比例函数图象在一次函数图象上方的部分,是反比例函数值大于一次函数值,可得答案;
(3)分两种情况:①点P在x轴上,作点A关于x轴的对称点A′(3,-2),连结A′B交x轴于点P,利用轴对称得出AP+BP的最小值为线段A′B,进而利用待定系数法求出解析式,即可得出P点坐标;②点P在y轴上,作点B关于y轴的对称点B′(-1,6),连结AB′交y轴于点P,利用轴对称得出AP+BP的最小值为线段AB′,进而利用待定系数法求出解析式,即可得出P点坐标.
解答:解:(1)由题意得:
,
解之得:
,
,
∴A、B两点坐标分别为A(3,2)、B(1,6);
(2)由图象得:不等式
>-2x+8的解集为0<x<1或x>3;
 (3)分两种情况:
(3)分两种情况:
①如果点P在x轴上,
作点A关于x轴的对称点A′(3,-2),连结A′B交x轴于点P,则PA′=PA,
所以AP+BP=A′P+BP=A′B,即AP+BP的最小值为线段A′B的长度.
设直线A′B的解析式为y=kx+b,
∵A′(3,-2),B(1,6),
∴
,解得
,
∴直线A′B的解析式为y=-4x+10,
当y=0时,x=
,
∴点P的坐标为(
,0);
 ②如果点P在y轴上,
②如果点P在y轴上,
作点B关于y轴的对称点B′(-1,6),连结AB′交y轴于点P,则PB′=PB,
所以AP+BP=AP+B′P=AB′,即AP+BP的最小值为线段AB′的长度.
设直线AB′的解析式为y=mx+n,
∵A(3,2),B′(-1,6),
∴
,解得
,
∴直线AB′的解析式为y=-x+5,
当x=0时,y=5,
∴点P的坐标为(0,5).
综上所述,点P的坐标为(
,0)或(0,5).
故答案为(3,2),(1,6);0<x<1或x>3.
|
解之得:
|
|
∴A、B两点坐标分别为A(3,2)、B(1,6);
(2)由图象得:不等式
| 6 |
| x |
 (3)分两种情况:
(3)分两种情况:①如果点P在x轴上,
作点A关于x轴的对称点A′(3,-2),连结A′B交x轴于点P,则PA′=PA,
所以AP+BP=A′P+BP=A′B,即AP+BP的最小值为线段A′B的长度.
设直线A′B的解析式为y=kx+b,
∵A′(3,-2),B(1,6),
∴
|
|
∴直线A′B的解析式为y=-4x+10,
当y=0时,x=
| 5 |
| 2 |
∴点P的坐标为(
| 5 |
| 2 |
 ②如果点P在y轴上,
②如果点P在y轴上,作点B关于y轴的对称点B′(-1,6),连结AB′交y轴于点P,则PB′=PB,
所以AP+BP=AP+B′P=AB′,即AP+BP的最小值为线段AB′的长度.
设直线AB′的解析式为y=mx+n,
∵A(3,2),B′(-1,6),
∴
|
|
∴直线AB′的解析式为y=-x+5,
当x=0时,y=5,
∴点P的坐标为(0,5).
综上所述,点P的坐标为(
| 5 |
| 2 |
故答案为(3,2),(1,6);0<x<1或x>3.
点评:此题主要考查了反比例函数与一次函数的交点问题,轴对称-最短路线问题,待定系数法求一次函数解析式,进行分类讨论、利用数形结合以及方程思想是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
下列各组数中互为相反数的是( )
| A、+(+5)与-(-5) | ||
| B、+(-5)与-(+5) | ||
C、+(+5)与-(-
| ||
| D、+(-5)与-(-5) |
下列几何体的截面不可能是圆的是( )
| A、棱柱 | B、圆锥 | C、球 | D、圆柱 |
 如图,把△ABC绕C顺时针旋转35°,得到△A′B′C,若∠BCA′=100°,则∠B′CA=
如图,把△ABC绕C顺时针旋转35°,得到△A′B′C,若∠BCA′=100°,则∠B′CA=