题目内容
某一电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.
(1)求月销售量y(台)与售价(x元/台)之间的函数关系式;
(2)若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.求售价x的取值范围;
(3)在(2)的条件下,当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
(1)求月销售量y(台)与售价(x元/台)之间的函数关系式;
(2)若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.求售价x的取值范围;
(3)在(2)的条件下,当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)根据题中条件销售价每降低10元,月销售量就可多售出50台,即可列出函数关系式;
(2)根据供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售即可求出x的取值.
(3)用x表示y,然后再用x来表示出w,根据函数关系式,即可求出最大w;
(2)根据供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售即可求出x的取值.
(3)用x表示y,然后再用x来表示出w,根据函数关系式,即可求出最大w;
解答:解:(1)根据题中条件销售价每降低10元,月销售量就可多售出50台,
则月销售量y(台)与售价x(元/台)之间的函数关系式:y=200+50×
,化简得:y=-5x+2200;
(2)∵供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台,
∴
,
解得:300≤x≤350.
∴y与x之间的函数关系式为:y=-5x+2200(300≤x≤350);
(3)W=(x-200)(-5x+2200),
整理得:W=-5(x-320)2+72000.
∵x=320在300≤x≤350内,
∴当x=320时,最大值为72000,
即售价定为320元/台时,商场每月销售这种空气净化器所获得的利润w最大,最大利润是72000元.
则月销售量y(台)与售价x(元/台)之间的函数关系式:y=200+50×
| 400-x |
| 10 |
(2)∵供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台,
∴
|
解得:300≤x≤350.
∴y与x之间的函数关系式为:y=-5x+2200(300≤x≤350);
(3)W=(x-200)(-5x+2200),
整理得:W=-5(x-320)2+72000.
∵x=320在300≤x≤350内,
∴当x=320时,最大值为72000,
即售价定为320元/台时,商场每月销售这种空气净化器所获得的利润w最大,最大利润是72000元.
点评:本题主要考查对于二次函数的应用和掌握,而且还应用到将函数变形求函数极值的知识,解题的关键是能够从实际问题中整理出二次函数模型,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个多边形有五条对角线,则这个多边形的边数为( )
| A、8 | B、7 | C、6 | D、5 |
 如图,点B,F,C,E在同一条直线上,∠A=∠D,FG=GC,若AB=6cm,BC=8cm,CE=DE=3cm,求线段FC的长.
如图,点B,F,C,E在同一条直线上,∠A=∠D,FG=GC,若AB=6cm,BC=8cm,CE=DE=3cm,求线段FC的长. 如图,把△ABC绕C顺时针旋转35°,得到△A′B′C,若∠BCA′=100°,则∠B′CA=
如图,把△ABC绕C顺时针旋转35°,得到△A′B′C,若∠BCA′=100°,则∠B′CA=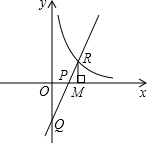 如图,直线y=kx-1(k>0)与双曲线y=
如图,直线y=kx-1(k>0)与双曲线y=