题目内容
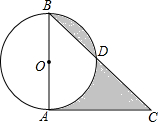 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则阴影部分的面积为
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则阴影部分的面积为考点:切线的性质,扇形面积的计算
专题:
分析:连接AD,先证AC=AB,再证明AD=BD,得出
=
,阴影部分的面积等于△ADC的面积,即可得出结果.
 |
| AD |
 |
| BD |
解答:解:连接AD;如图所示:
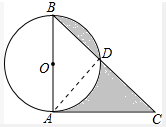 ∵CA是⊙O的切线,
∵CA是⊙O的切线,
∴AB⊥AC,
∴∠BAC=90°,
∵∠C=45°,
∴∠B=90°-45°=45°,
∴AC=AB=2,
∵AB是直径,
∴∠ADB=90°,
即AD⊥BC,
∴CD=BD,
∴AD=
BC=BD=CD,
∴
=
,
∴S阴影=S△ADC=
S△ABC=
×
×2×2=1.
故答案为:1.
 ∵CA是⊙O的切线,
∵CA是⊙O的切线,∴AB⊥AC,
∴∠BAC=90°,
∵∠C=45°,
∴∠B=90°-45°=45°,
∴AC=AB=2,
∵AB是直径,
∴∠ADB=90°,
即AD⊥BC,
∴CD=BD,
∴AD=
| 1 |
| 2 |
∴
 |
| AD |
 |
| BD |
∴S阴影=S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:1.
点评:本题考查了切线的性质和扇形面积的计算方法;证出阴影部分的面积=△ADC的面积是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列几何体的截面不可能是圆的是( )
| A、棱柱 | B、圆锥 | C、球 | D、圆柱 |
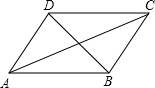 如图,四边形ABCD是平行四边形,下列说法不正确的是( )
如图,四边形ABCD是平行四边形,下列说法不正确的是( )| A、当AC=BD时,四边形ABCD是矩形 |
| B、当∠DAB=90°时,四边形ABCD是正方形 |
| C、当AC⊥BD时,四边形ABCD是菱形 |
| D、当AB=BC时,四边形ABCD是菱形 |
 如图,把△ABC绕C顺时针旋转35°,得到△A′B′C,若∠BCA′=100°,则∠B′CA=
如图,把△ABC绕C顺时针旋转35°,得到△A′B′C,若∠BCA′=100°,则∠B′CA=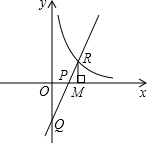 如图,直线y=kx-1(k>0)与双曲线y=
如图,直线y=kx-1(k>0)与双曲线y=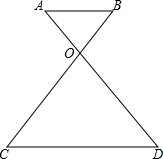 如图,AD与BC交与点O,且AB∥CD.
如图,AD与BC交与点O,且AB∥CD.