题目内容
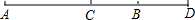 如图,C为线段AD上一点,点B为CD的中点,且AD=12cm,AC=4BC.
如图,C为线段AD上一点,点B为CD的中点,且AD=12cm,AC=4BC.(1)图中共有
(2)求AC的长;
(3)若点E在直线AD上,且EA=7cm,求BE的长.
考点:两点间的距离
专题:
分析:(1)根据直线上线段的条数公式:直线上有n个点,线段的条数是
,可得答案;
(2)根据线段中点的性质,可用BC表示CD,根据线段的和差,可得关于BC的方程,根据解方程,可得BC的长,AC的长;
(3)分类讨论:点E在线段AD上,点E在线段AD的延长线上,根据线段的和差,可得答案.
| n(n-1) |
| 2 |
(2)根据线段中点的性质,可用BC表示CD,根据线段的和差,可得关于BC的方程,根据解方程,可得BC的长,AC的长;
(3)分类讨论:点E在线段AD上,点E在线段AD的延长线上,根据线段的和差,可得答案.
解答:解:(1)图中有四个点,线段有
=6,
故答案为:6;
(2)由点B为CD的中点,得
CD=2BC=2BD,
由线段的和差,得
AD=AC+CD,即4BC+2BC=12,
解得BC=2cm,
AC=4BC=4×2=8cm;
(3)①当点E在线段AD上时,由线段的和差,得
AB=AC+BC=8+2=10cm
BE=AB-AE=10-7=3cm,
②当点E在线段AD的延长线上时,由线段的和差,得
AB=AC+BC=8+2=10cm
BE=AB+AE=10+7=17cm,
综上所述:BE的长为3cm或17cm.
| 4×(4-1) |
| 2 |
故答案为:6;
(2)由点B为CD的中点,得
CD=2BC=2BD,
由线段的和差,得
AD=AC+CD,即4BC+2BC=12,
解得BC=2cm,
AC=4BC=4×2=8cm;
(3)①当点E在线段AD上时,由线段的和差,得
AB=AC+BC=8+2=10cm
BE=AB-AE=10-7=3cm,
②当点E在线段AD的延长线上时,由线段的和差,得
AB=AC+BC=8+2=10cm
BE=AB+AE=10+7=17cm,
综上所述:BE的长为3cm或17cm.
点评:本题考查了两点间的距离,利用了直线上线段的条数公式:直线上有n个点,线段的条数是
;(2)利用了线段中点的性质,线段的和差;(3)分类讨论是解题关键.
| n(n-1) |
| 2 |

练习册系列答案
相关题目
下列各组数中互为相反数的是( )
| A、+(+5)与-(-5) | ||
| B、+(-5)与-(+5) | ||
C、+(+5)与-(-
| ||
| D、+(-5)与-(-5) |
下列实数中是无理数的是( )
A、
| ||
| B、π | ||
| C、0.141414 | ||
D、-
|
 如图,已知在平行四边形ABCD中,AB=4,BC=6,AD到BC的距离AE=2,则AB到CD的距离AF的长是
如图,已知在平行四边形ABCD中,AB=4,BC=6,AD到BC的距离AE=2,则AB到CD的距离AF的长是 如图,点B,F,C,E在同一条直线上,∠A=∠D,FG=GC,若AB=6cm,BC=8cm,CE=DE=3cm,求线段FC的长.
如图,点B,F,C,E在同一条直线上,∠A=∠D,FG=GC,若AB=6cm,BC=8cm,CE=DE=3cm,求线段FC的长.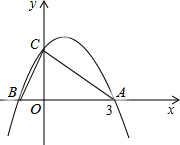 如图,抛物线y=-x2+2x+m与x轴相交于点A(3,0)和B,与y轴相交于点C.
如图,抛物线y=-x2+2x+m与x轴相交于点A(3,0)和B,与y轴相交于点C.