题目内容
10. 如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠B=( )
如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠B=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
分析 根据等边对等角和三角形内角和定理可得∠D的度数,再根据在同圆或等圆中,同弧或等弧所对的圆周角相等可得答案.
解答 解:∵CA=CD,且∠ACD=40°,
∴∠ADC=70°,
∴∠B=∠D=70°,
故选:D.
点评 此题主要考查了圆周角定理,关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.甲、乙两人骑自行车比赛,若甲先骑30分钟,则乙出发后50分钟可追上甲,设甲、乙每小时分别骑x千米、y千米,则可列方程( )
| A. | 30x=50y | B. | $\frac{1}{2}x=({\frac{1}{2}+\frac{5}{6}})y$ | C. | (30+50)x=50y | D. | $({\frac{1}{2}+\frac{5}{6}})x=\frac{5}{6}y$ |
4.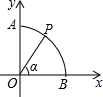 如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
 如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )| A. | (sinα,sinα) | B. | (cosα,cosα) | C. | (sinα,cosα) | D. | (cosα,sinα) |
1.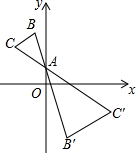 如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )
如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )
 如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )
如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )| A. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n+3) | B. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n-3) | C. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n+2) | D. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n-2) |
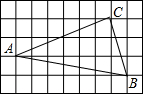 如图,在9×5的正方形网格中,每个小正方形边长均为1,△ABC的顶点均在格点上.
如图,在9×5的正方形网格中,每个小正方形边长均为1,△ABC的顶点均在格点上. 如图,已知CD∥BF,∠B+∠D=180°,求证:AB∥DE.
如图,已知CD∥BF,∠B+∠D=180°,求证:AB∥DE.