题目内容
18.设a,b是一个直角三角形两条直角边的长,且(a2+b2)(a2+b2+1)=20,则这个直角三角形的斜边长为2.分析 将a2+b2看做整体解方程得a2+b2=4或a2+b2=-5(舍),从而得出c2=a2+b2=4,即可得答案.
解答 解:∵(a2+b2)(a2+b2+1)=20,
∴(a2+b2)2+(a2+b2)-20=0,
∴(a2+b2-4)(a2+b2+5)=0,
解得:a2+b2=4或a2+b2=-5(舍),
则c2=a2+b2=4,
∴这个直角三角形的斜边长为2,
故答案为:2.
点评 本题主要考查解一元二次方程的能力和勾股定理,熟练掌握解一元二次方程的几种常用方法是解题的关键.

练习册系列答案
相关题目
8.过⊙O内一点M的最长的弦长为6厘米,最短的弦长为4厘米,则OM的长为( )
| A. | $\sqrt{3}$厘米 | B. | $\sqrt{5}$厘米 | C. | 2厘米 | D. | 5厘米 |
13.5的倒数是( )
| A. | 5 | B. | -5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
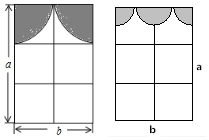 如图,小红和小兰房间窗户的装饰物分别由一些半圆和四分之一圆组成(半径分别相同).
如图,小红和小兰房间窗户的装饰物分别由一些半圆和四分之一圆组成(半径分别相同).
 如图,在△ABC中,DE是中位线
如图,在△ABC中,DE是中位线