如图.在△ABC中.∠C=90°.AB=5.AC=3.则tanB的值为( )A．$\frac{4}{3}$B．$\frac{3}{4}$C．$\frac{3}{5}$D．$\frac{4}{5}$ 题目和参考答案——青夏教育精英家教网—

题目内容

2．

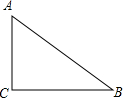如图，在△ABC中，∠C=90°，AB=5，AC=3，则tanB的值为（　　）

A．

$\frac{4}{3}$

B．

$\frac{3}{4}$

C．

$\frac{3}{5}$

D．

$\frac{4}{5}$

分析根据勾股定理，可得BC的长，根据正切函数是对边比邻边，可得答案．

解答解：由勾股定理，得
BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4．
tanB=$\frac{AC}{BC}$=$\frac{3}{4}$，
故选：B．

点评本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．

练习册系列答案

相关题目

12．若扇形面积为15πcm²，半径为6cm，则扇形的弧长是5πcm．

13．某商店的一种商品的进价降低了8%，而售价保持不变，可使得商店的利润率提10%，原来的利润率为15%．

10．把一边长为30cm的正方形硬纸板四角各剪一个同样大小的正方形，将剩余部分折成一个无盖的长方体形状的盒子（纸板的厚度忽略不计）．
①要使折成的长方体盒子的底面积为576m²，那么剪掉的正方形的边长是多少？
②折成的长方体盒子的侧面积是否有最大值？如果有，求出这个最大值和此时剪掉的正方形的边长；如果没有，说明理由．

17．若x+$\frac{1}{x}=3$，则$\frac{3x}{{x}^{2}+x+1}$的值是$\frac{3}{4}$．

7．（1）解方程：$\frac{5}{{x}^{2}-1}$+$\frac{x}{x-1}$=$\frac{x-4}{x+1}$；
（2）图①②均为7×6的正方形网络，点A，B，C在格点上．
（a）在图①中确定格点D，并画出以A、B、C、D为顶点的四边形，使其为轴对称图形（画一个即可）．
（b）在图②中确定格点E，并画出以A、B、C、E为顶点的四边形，使其为中心对称图形（画一个即可）

14．己知sinα=$\frac{2}{3}$，则（　　）

11．冬季的一天，室外温度为-9℃，室内的温度是20℃，则室内外温度相差（　　）

12．

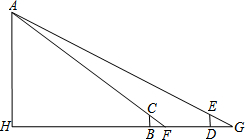如图，要测量建筑物AH的高度，可以采用以下方法：立两根高2米长的标杆BC和DE，两杆之间的距离BD=20米，并使D，B，H三点在一条直线上；从点B处退行5米到点F处，人的眼睛贴着地面观察A点，使A，C，F三点成一线；从D处退行6米到点G处，从G观察A点，使A，E，G三点也成一线．请你利用以上的信息计算出AH的高度（测量过程中，建筑物AH，标杆BC和DH均与地面垂直）．

试题分类