题目内容
10.把一边长为30cm的正方形硬纸板四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方体形状的盒子(纸板的厚度忽略不计).①要使折成的长方体盒子的底面积为576m2,那么剪掉的正方形的边长是多少?
②折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.

分析 ①设剪掉的正方形边长为xcm,则折成的长方体盒子地面正方形边长为(30-2x),根据正方形面积=边长的平方列出方程求解即可;
②根据侧面积=4×长方体的长×高列出函数关系式,配方可得其最大值.
解答 解:①设剪掉的正方形边长为xcm,则折成的长方体盒子地面正方形边长为(30-2x)cm,
根据题意,得:(30-2x)2=576,
解得:x=3或x=27(舍去),
故剪掉的正方形的边长是3cm;
②根据题意知,侧面矩形的长为(30-2x)cm,宽为xcm,
则长方体盒子的侧面积S=4x(30-2x)=-8x2+120x=-8(x-$\frac{15}{2}$)2+450,
∴当x=$\frac{15}{2}$时,S取得最大值,最大值为450,
答:当剪掉的正方形的边长为$\frac{15}{2}$cm时,长方体盒子的侧面积有最大值450cm2.
点评 本题主要考查一元二次方程、二次函数的实际应用能力,根据题意列出方程或函数关系式是关键.

练习册系列答案
相关题目
20.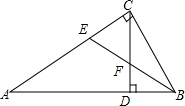 如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )
如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )
①∠CFE=∠CEF;②∠FCB=∠FBC,③∠A=∠DCB;④∠CFE与∠CBF互余.
 如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )
如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的有( )①∠CFE=∠CEF;②∠FCB=∠FBC,③∠A=∠DCB;④∠CFE与∠CBF互余.
| A. | ①③④ | B. | ②③④ | C. | ①②④ | D. | ①②③ |
1.下列长度的各组线段中,能构成三角形的是( )
| A. | 3,4,5 | B. | 2,2,4 | C. | 1,2,3 | D. | 2,3,6 |
18.下列函数中(x是自变量)是二次函数的是( )
| A. | y=-$\frac{1}{2}+$x+$\frac{1}{x}$ | B. | y=1+x+5x2 | C. | y=22+2x | D. | y=$\frac{1}{2}{x}^{3}-{x}^{2}+25$ |
2.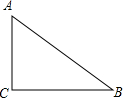 如图,在△ABC中,∠C=90°,AB=5,AC=3,则tanB的值为( )
如图,在△ABC中,∠C=90°,AB=5,AC=3,则tanB的值为( )
 如图,在△ABC中,∠C=90°,AB=5,AC=3,则tanB的值为( )
如图,在△ABC中,∠C=90°,AB=5,AC=3,则tanB的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
19.下列说法正确的是( )
| A. | 一组对边平行且有一组邻边相等的四边形是平行四边形 | |
| B. | 同一边上的两个角相等的梯形是等腰梯形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |
 如图,OP=1,过P作PP1⊥OP且PP1=1,根据勾股定理,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…;依此继续,得OP2014=$\sqrt{2015}$.
如图,OP=1,过P作PP1⊥OP且PP1=1,根据勾股定理,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…;依此继续,得OP2014=$\sqrt{2015}$.