题目内容
7．（1）解方程：$\frac{5}{{x}^{2}-1}$+$\frac{x}{x-1}$=$\frac{x-4}{x+1}$；（2）图①②均为7×6的正方形网络，点A，B，C在格点上．
（a）在图①中确定格点D，并画出以A、B、C、D为顶点的四边形，使其为轴对称图形（画一个即可）．
（b）在图②中确定格点E，并画出以A、B、C、E为顶点的四边形，使其为中心对称图形（画一个即可）
分析 （1）化分式方程为整式方程，然后解方程，注意要验根；
（2）可画出一个等腰梯形，则是轴对称图形；
（3）画一个矩形，则是中心对称图形．
解答 解：（1）由原方程，得5+x（x+1）=（x+4）（x-1），
整理，得2x=9，
解得x=4.5；
（2）如图①所示：等腰梯形ABCD为轴对称图形；
；
（3）如图②所示：矩形ABDC为轴对称图形；
．
点评 此题比较灵活的考查了等腰梯形、矩形的对称性，是道好题．
练习册系列答案
阅读快车系列答案
相关题目
18．下列函数中（x是自变量）是二次函数的是（ ）
| A． | y=-$\frac{1}{2}+$x+$\frac{1}{x}$ | B． | y=1+x+5x2 | C． | y=22+2x | D． | y=$\frac{1}{2}{x}^{3}-{x}^{2}+25$ |
2．
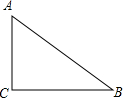如图，在△ABC中，∠C=90°，AB=5，AC=3，则tanB的值为（ ）
如图，在△ABC中，∠C=90°，AB=5，AC=3，则tanB的值为（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
12．已知正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象的一个交点坐标是（1，3），则另一个交点的坐标是（ ）
| A． | （-1，-3） | B． | （-3，-1） | C． | （-1，-2） | D． | （-2，-3） |
19．下列说法正确的是（ ）
| A． | 一组对边平行且有一组邻边相等的四边形是平行四边形 | |
| B． | 同一边上的两个角相等的梯形是等腰梯形 | |
| C． | 等边三角形既是轴对称图形又是中心对称图形 | |
| D． | 对角线互相垂直平分的四边形是菱形 |
