题目内容
11．
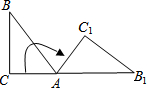如图，在三角形ABC中，∠C=90°，∠B=35°，将三角形ABC绕点A按顺时针方向旋转到三角形AB1C1的位置，使得点C、A、B1在一条直线上，那么旋转角等于（ ）| A． | 145° | B． | 125° | C． | 70° | D． | 55° |
分析 根据三角形内角和定理求出∠BAC的度数，根据旋转变换的性质求出∠BAC1=70°，得到∠CAC的度数即可．
解答 解：∵∠C=90°，∠B=35°，
∴∠BAC=55°，
由旋转的性质可知，∠B1AC1=∠BAC=55°，
∴∠BAC1=70°，
∴∠CAC1=125°，
故选：B．
点评 本题考查的是旋转变换的性质、三角形内角和定理的应用，旋转变换的性质：对应点与旋转中心所连线段的夹角等于旋转角，旋转前、后的图形全等．
练习册系列答案
相关题目
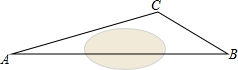在一次课外实践活动中，同学们要测量某公园人工湖两侧A，B两个凉亭之间的距离．如图，现测得∠ABC=30°，∠CAB=15°，AC=200米，请计算A，B两个凉亭之间的距离（结果精确到1米）（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）
3．下面哪个点在函数y=$\frac{1}{2}$x+1的图象上（ ）
| A． | （-2，0） | B． | （-2，1） | C． | （2，0） | D． | （2，1） |
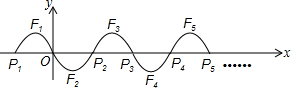如图，在平面直角坐标系xOy中，二次函数y=-x2-2x图象位于x轴上方的部分记作F1，与x轴交于点P1和O；F2与F1关于点O对称，与x轴另一个交点为P2；F3与F2关于点P2对称，与x轴另一个交点为P3；…．这样依次得到F1，F2，F3，…，Fn，则Fn的顶点坐标为[2n-3，（-1）n+1]（n为正整数，用含n的代数式表示）．