题目内容
17.已知一次函数y=kx+b的图象经过点A(-1,-1)和点B(1,-3).求:(1)直接写出一次函数的表达式y=-x-2;
(2)直接写出直线AB与坐标轴围成的三角形的面积2;
(3)请在x轴上找到一点P,使得PA+PB最小,并求出P的坐标.
分析 (1)把A、B两点代入可求得k、b的值,可得到一次函数的表达式;
(2)分别令y=0、x=0可求得直线与两坐标轴的两交点坐标,可求得所围成的三角形的面积;
(3)根据轴对称的性质,找到点A关于x的对称点A′,连接BA′,则BA′与x轴的交点即为点P的位置,求出直线BA′的解析式,可得出点P的坐标.
解答 解:(1)∵一次函数y=kx+b的图象经过点A(-1,-1)和点B(1,-3),
∴$\left\{\begin{array}{l}{-k+b=-1}\\{k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=-2}\end{array}\right.$,
∴一次函数为y=-x-2;
(2)在y=-x-2中,分别令x=0、y=0,
可求得一次函数与两坐标轴的交点坐标分别为(0,-2)、(-2,0),
∴直线与两坐标轴围成的三角形的面积为:S=$\frac{1}{2}$×2×2=2;
(3)作点A关于x轴的对称点A′,连接BA′与x轴 的交点即为点P.
设直线BA′的解析式为y=mx+n,
将点A′(-1,1)和点B(1,-3)代入可得:
$\left\{\begin{array}{l}{-m+n=1}\\{m+n=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-2}\\{n=-1}\end{array}\right.$.
故直线BA′的解析式为y=-2x-1,
令y=0,可得-2x-1=0,
解得:x=-$\frac{1}{2}$,
故点P的坐标为(-$\frac{1}{2}$,0).
故答案为y=-x-2;2.
点评 本题考查了待定系数法求函数解析式,一次函数图象上点的坐标特征,轴对称-最短路线问题,掌握待定系数法的应用是解题的关键.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2$\sqrt{2}$,AC=3$\sqrt{2}$,BC=6,则⊙O的半径是( )
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2$\sqrt{2}$,AC=3$\sqrt{2}$,BC=6,则⊙O的半径是( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
 如图,AB是半圆的直径,点C、D是半圆上两点,∠ADC=128°,则∠ABC=52°.
如图,AB是半圆的直径,点C、D是半圆上两点,∠ADC=128°,则∠ABC=52°.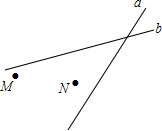 如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.
如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案. 甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.