题目内容
3．如果直线y=kx+b（k＞0）是由正比例函数y=kx的图象向左平移1个单位得到，那么不等式kx+b＞0的解集是x＞-1．分析 直接利用一次函数平移规律得出图象平移后与x轴交点，进而得出答案．
解答 解：∵直线y=kx+b（k＞0）是由正比例函数y=kx的图象向左平移1个单位得到，
∴y=kx+b经过（-1，0），
∴不等式kx+b＞0的解集是：x＞-1．
故答案为：x＞-1．
点评 此题主要考查了一次函数的几何变换以及一次函数与一元一次方程的应用不等式，正确得出图象与x轴交点是解题关键．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
18．已知两组数据，2、3、4和3、4、5，那么下列说法正确的是（ ）
| A． | 中位数不相等，方差不相等 | B． | 平均数相等，方差不相等 | ||
| C． | 中位数不相等，平均数相等 | D． | 平均数不相等，方差相等 |
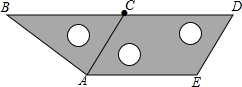如图，将三个相同的三角板不重叠不留空隙地拼在一起，观察图形，在线段AB，BD，DE，EC，CA，AE中，相互平行的线段有（ ）
9．
如图，⊙O与Rt△ABC的斜边AB相切于点D，与直角边AC相交于点E，且DE∥BC．已知AE=2$\sqrt{2}$，AC=3$\sqrt{2}$，BC=6，则⊙O的半径是（ ）
如图，⊙O与Rt△ABC的斜边AB相切于点D，与直角边AC相交于点E，且DE∥BC．已知AE=2$\sqrt{2}$，AC=3$\sqrt{2}$，BC=6，则⊙O的半径是（ ）| A． | 3 | B． | 2$\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | $\sqrt{6}$ |