题目内容
1.若代数式$\frac{x+1}{x-2}÷\frac{x+3}{x+4}$有意义,则x的取值范围是x≠2,x≠-3,x≠-4.分析 根据分式的分母不为0且除式不为0,确定出x的范围即可.
解答 解:要使代数式$\frac{x+1}{x-2}÷\frac{x+3}{x+4}$有意义,须有x-2≠0,x+3≠0,x+4≠0,
则x的范围是x≠2,x≠-3,x≠-4.
故答案为:x≠2,x≠-3,x≠-4
点评 此题考查了分式的乘除法,以及分式有意义的条件,弄清分式有意义的条件是解本题的关键.

练习册系列答案
相关题目
16.计算$\sqrt{4}$的结果是( )
| A. | -2 | B. | ±2 | C. | 2 | D. | 4 |

 现有边长为4cm的正方形纸片ABCD,点P在AD上,将正方形纸片ABCD折叠使点B落在点P处,点C落在点H处,PH与CD交于点G,折痕为EF,连接EG.
现有边长为4cm的正方形纸片ABCD,点P在AD上,将正方形纸片ABCD折叠使点B落在点P处,点C落在点H处,PH与CD交于点G,折痕为EF,连接EG. 如图,直线AB、CD相交于点O,∠AOE=∠DOE,∠BOE=150°,求∠BOD的度数.
如图,直线AB、CD相交于点O,∠AOE=∠DOE,∠BOE=150°,求∠BOD的度数.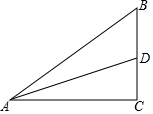 如图所示,在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线.
如图所示,在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线.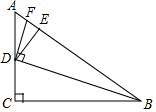 如图,△ABC中,∠ACB=90°,tanA=$\sqrt{2}$,点D是边AC上一点,连接BD,并将
如图,△ABC中,∠ACB=90°,tanA=$\sqrt{2}$,点D是边AC上一点,连接BD,并将