题目内容
18.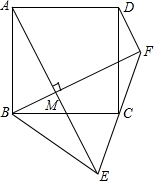 正方形ABCD中,点C为线段EF的中点,连接AE、BF交于M,当AE⊥BF,∠BFE=45°,BE=10,则DF的长为2$\sqrt{5}$.
正方形ABCD中,点C为线段EF的中点,连接AE、BF交于M,当AE⊥BF,∠BFE=45°,BE=10,则DF的长为2$\sqrt{5}$.
分析 (1)作CG⊥BF于G,连接CM.只要证明△MCF,△MCG,△GCF都是等腰直角三角形,由△ABM≌△BCG,推出BM=CG=GM=GF,AM=BG,由ME=MF=BG,推出AM=ME,由BM⊥AE,推出AB=BE=10,设BM=x,则AM=2x,在Rt△ABM中,根据AB2=AM2+BM2,列出方程即可解决问题.
解答 解:如图,作CG⊥BF于G,连接CM.
∵AE⊥BF,
∴∠EMF=90°,∵CE=CF,
∴CM=CF=CE,
∵∠CGF=90°,∠CFG=45°,
∴∠CMF=∠CFM=45°,
∴∠MCF=∠BCD=90°,
∴∠BCM=∠DCF,CG=GM=GF,
∵CB=CD,CM=CF,
∴△BCM≌△DCF,
∴BM=DF,
易证△ABM≌△BCG,
∴BM=CG=GM=GF,AM=BG,
∵ME=MF=BG,
∴AM=ME,∵BM⊥AE,
∴AB=BE=10,
设BM=x,则AM=2x,
在Rt△ABM中,∵AB2=AM2+BM2,
∴102=x2+(2x)2,
∴x=2$\sqrt{5}$,
∴DF=AM=2$\sqrt{5}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.

练习册系列答案
相关题目
7.甲、乙、丙三位选手各射击10次的成绩统计如下:
其中,发挥最稳定的选手是丙.
| 选手 | 甲 | 乙 | 丙 |
| 平均数(环) | 9.3 | 9.3 | 9.3 |
| 方差(环2) | 0.25 | 0.38 | 0.14 |
 如图,直线AB、CD相交于点O,∠AOE=∠DOE,∠BOE=150°,求∠BOD的度数.
如图,直线AB、CD相交于点O,∠AOE=∠DOE,∠BOE=150°,求∠BOD的度数.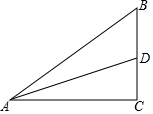 如图所示,在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线.
如图所示,在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线.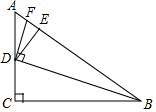 如图,△ABC中,∠ACB=90°,tanA=$\sqrt{2}$,点D是边AC上一点,连接BD,并将
如图,△ABC中,∠ACB=90°,tanA=$\sqrt{2}$,点D是边AC上一点,连接BD,并将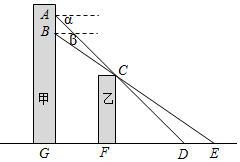 小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.
小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.