题目内容
16.计算:(1)(-2)2-$\sqrt{12}$+(-3)0-($\frac{1}{3}$)-2
(2)$\frac{2x}{x+1}$-$\frac{2x+4}{{x}^{2}-1}$÷$\frac{x+2}{{x}^{2}-2x+1}$.
分析 (1)根据零指数幂以及负整数幂的意义即可求出答案.
(2)根据分式的运算法则即可求出答案.
解答 解:(1)原式=4-2$\sqrt{3}$+1-9
=-4-2$\sqrt{3}$.
(2)原式=$\frac{2x}{x+1}$-$\frac{2(x+2)}{(x+1)(x-1)}$×$\frac{(x-1)^{2}}{x+2}$
=$\frac{2x}{x+1}$-$\frac{2(x-1)}{x+1}$
=$\frac{2}{x+1}$
点评 本题考查学生的计算能力,解题的关键是熟练运用运算法则,本题属于基础题型.

练习册系列答案
相关题目
7.甲、乙、丙三位选手各射击10次的成绩统计如下:
其中,发挥最稳定的选手是丙.
| 选手 | 甲 | 乙 | 丙 |
| 平均数(环) | 9.3 | 9.3 | 9.3 |
| 方差(环2) | 0.25 | 0.38 | 0.14 |
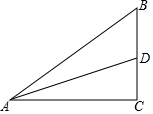 如图所示,在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线.
如图所示,在Rt△ACB中,∠C=90°,AC=3,BC=2,AD为中线. 如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,点M运动的路径长为4π.
如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,点M运动的路径长为4π.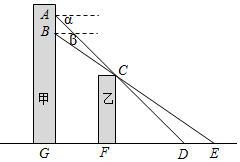 小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.
小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.