题目内容
20.若A(-$\frac{13}{4}$,y1),B(-$\frac{5}{4}$,y2),C($\frac{1}{4}$,y3)为二次函数y=x2+4x-5的图象上的三点,试比较y1、y2、y3的大小.分析 将二次函数y=x2+4x-5配方,求对称轴,再根据A、B、C三点与对称轴的位置关系,开口方向判断yl,y2,y3的大小.
解答 解:∵y=x2+4x-5=(x+2)2-9,
∴抛物线开口向上,对称轴为x=-2,
∵A、B、C三点中,B点离对称轴最近,C点离对称轴最远,
∴y2<y1<y3.
点评 本题考查了二次函数的增减性.当二次项系数a>0时,在对称轴的左边,y随x的增大而减小,在对称轴的右边,y随x的增大而增大;a<0时,在对称轴的左边,y随x的增大而增大,在对称轴的右边,y随x的增大而减小.

练习册系列答案
相关题目
10.-$\frac{1}{2016}$的绝对值是( )
| A. | -2016 | B. | $\frac{1}{2016}$ | C. | -$\frac{1}{2016}$ | D. | 2016 |
8. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①abc<0;②b=-2a;③b2+4ac>0;④4a+2b+c<0.
其中结论正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc<0;②b=-2a;③b2+4ac>0;④4a+2b+c<0.
其中结论正确的是( )
| A. | ①② | B. | ①②③ | C. | ①②③④ | D. | ②③④ |
12.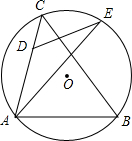 如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )
如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )
 如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )
如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 已知菱形ABCD,AB=4,∠B=60°,以点D为圆心作⊙D与直线AB相切于点G,连接DG.
已知菱形ABCD,AB=4,∠B=60°,以点D为圆心作⊙D与直线AB相切于点G,连接DG.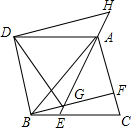 如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.
如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.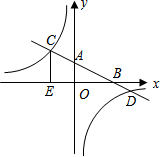 如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.