题目内容
19.下列各式的变形中,错误的是( )| A. | 2x+8=0变形为2x=-8 | B. | $\frac{x-2}{3}$=x+1变形为x-2=3x+3 | ||
| C. | -2(x-3)=-2变形为x-3=1 | D. | -$\frac{x+2}{3}$=1变形为-x+2=3 |
分析 根据等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.
解答 解:A、两边都减8,故A正确;
B、两边都乘以3,故B正确;
C、两边都除以-2,故C正确;
D、两边都乘以3,-x-2=3,故D错误;
故选:D.
点评 本题主要考查了等式的基本性质,等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.

练习册系列答案
相关题目
14.对于抛物线y=-$\frac{1}{2}$x2-3,下列说法错误的是( )
| A. | 抛物线的开口向下 | |
| B. | 对称轴为直线x=-3 | |
| C. | 顶点坐标为(0,-3) | |
| D. | 抛物线y=-$\frac{1}{2}$x2-3与y=$\frac{1}{2}$(x+1)2+1开口大小相同 |
11.下列各数是方程5x=4x+8的解是的是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
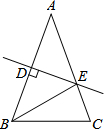 如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为30°.
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为30°.