题目内容
12.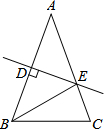 如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为30°.
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为30°.
分析 根据等腰三角形的性质求出∠ABC=∠C=70°,根据线段的垂直平分线的性质得到EA=EB,计算即可.
解答 解:∵AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=40°,
∴∠CBE=∠ABC-∠EBA=30°,
故答案为:30°.
点评 本题考查的是线段的垂直平分线的性质,线段的垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列各式的变形中,错误的是( )
| A. | 2x+8=0变形为2x=-8 | B. | $\frac{x-2}{3}$=x+1变形为x-2=3x+3 | ||
| C. | -2(x-3)=-2变形为x-3=1 | D. | -$\frac{x+2}{3}$=1变形为-x+2=3 |
7.下列各组数中,结果相等的为( )
| A. | -32与(-3)2 | B. | 32与-(-3)2 | C. | -33与(-3)3 | D. | (-3)3与-(-3)3 |
4.下列各组中的两个单项式中,是同类项的是( )
| A. | a2和-2a | B. | 2m2n和3nm2 | C. | -5ab和-5abc | D. | x3和23 |
2.下列各式不是同类项的是( )
| A. | -ab与3ab | B. | 2a2b与2ba2 | C. | 3x2y与xy2 | D. | -2与0 |
 AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=50°,则∠EDB=25°.
AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=50°,则∠EDB=25°. 如图,AB、CD是⊙O的两条直径,弦AE∥CD,
如图,AB、CD是⊙O的两条直径,弦AE∥CD,