题目内容
16.“新禧”杂货店去批发市场购买某种新型儿童玩具,第一次用1200元购得玩具若干个,并以7元的价格出售,很快就售完.由于该玩具深受儿童喜爱,第二次进货时每个玩具的批发价已比第一次提高了20%,他用1500元所购买的玩具数量比第一次多10个,再按8元售完,问该老板两次一共赚了多少钱?分析 设这种新型儿童玩具第一次进价为x元/个,则第二次进价为1.2x元/个,分别可以表示出第一次购买玩具的数量和第二次购买玩具的数量,根据两次购买玩具的数量之间的关系建立方程求出其解就可以了.
解答 解:设这种新型儿童玩具第一次进价为x元/个,则第二次进价为1.2x元/个,
根据题意,得$\frac{1500}{1.2x}$-$\frac{1200}{x}$=10,
变形为:1500-1440=12x,
解得:x=5,
经检验,x=5是原方程的解,
则该老板这两次购买玩具一共盈利为:$\frac{1500}{1.2×5}$(7-1.2×5)+$\frac{1200}{5}$×(7-5)=730(元).
答:该老板两次一共赚了730元.
点评 本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,解答时根据两次购买玩具的数量关系建立方程是关键.检验是解分式方程的必须过程,学生容易忘记.

练习册系列答案
相关题目
7.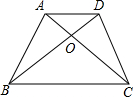 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果S△ACD:S△ABC=1:2,那么S△AOD:S△BOC是( )
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果S△ACD:S△ABC=1:2,那么S△AOD:S△BOC是( )
 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果S△ACD:S△ABC=1:2,那么S△AOD:S△BOC是( )
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,如果S△ACD:S△ABC=1:2,那么S△AOD:S△BOC是( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
4.若一元二次方程(2m+6)x2+m2-9=0的常数项是0,则m等于( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 9 |
11.反比例函数y=$\frac{k}{x}$的图象生经过点(1,-2),则k的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
1.下列运算中,正确的是( )
| A. | 3a-a=2 | B. | x+y=xy | C. | a2+a3=a5 | D. | xy-yx=0 |
8.在Rt△ABC中,若各边长都扩大3倍,则锐角A的正弦值( )
| A. | 不变 | B. | 扩大3倍 | C. | 缩小到原来的$\frac{1}{3}$ | D. | 不能确定 |
5.有如下四个事件:①篮球队员在罚球线上投篮一次,未投中;②任意画一个圆的内接四边形,这个四边形的对角互补;③经过有交通信号灯的路口,遇到红灯;④三角形的外心落在三角形的内部.上述事件中是随机事件的是( )
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
6.方程(x-1)(x+2)=x-1的解是( )
| A. | -2 | B. | 1,-2 | C. | -1,1 | D. | -1,3 |
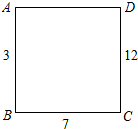 如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的
如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的