题目内容
如图，已知D，E分别是△ABC的AB，AC边上的点，DE∥BC，AM⊥BC，垂足为N，AM与DE相交于点N，S△ADE：S四边形DBCE=1：8，求AN：AM．考点：相似三角形的判定与性质
专题：
分析：先证明△ADE∽△ABC，由条件可求得其面积比，可求出其相似比，再利用相似三角形的性质可求得AN：AM．
解答：解：∵S△ADE：S四边形DBCE=1：8，
∴
=
，
∵DE∥BC，
∴△ADE∽△ABC，
∵AM⊥BC，
∴AN⊥DE，
∴
=
=
，
∴AN：AM=1：3．
∴
| S△ADE |
| S△ABC |
| 1 |
| 9 |
∵DE∥BC，
∴△ADE∽△ABC，
∵AM⊥BC，
∴AN⊥DE，
∴
| AN |
| AM |
|
| 1 |
| 3 |
∴AN：AM=1：3．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形对应高的比等于相似比是解题的关键．
练习册系列答案
相关题目
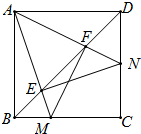已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N．连接B、D，使分别交AM、AN于E、F，求证：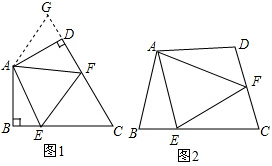
如图，若点C落在△ABC外，则2∠C=∠1+∠2的结论是否成立？若不成立，请写出正确的结论，并说明理由．