题目内容
求证:关于x的方程(k-3)x2+kx+1=0有实根.
考点:根的判别式,一元一次方程的解
专题:证明题
分析:分k-3=0,为一元一次方程,有一个实数根;k-3≠0,根据一元二次方程的根的判别式与0的关系来判断根的情况.
解答:证明:当k-3=0,kx+1=0为一元一次方程,有一个实数根;
k-3≠0,
∵△=b2-4ac
=k2-4(k-3)
=k2-4k+12
=(k-2)2+8>0,
∴方程有两个不相等的实数根.
综上所知,关于x的方程(k-3)x2+kx+1=0有实根.
k-3≠0,
∵△=b2-4ac
=k2-4(k-3)
=k2-4k+12
=(k-2)2+8>0,
∴方程有两个不相等的实数根.
综上所知,关于x的方程(k-3)x2+kx+1=0有实根.
点评:此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
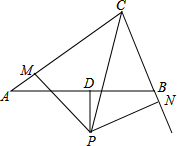 如图,在△ABC中,D为AB边的中点,DP⊥AB交∠ACB的平分线于点P,PM⊥AC于点M,PN⊥BC交CB的延长线于点N,求证:CM=BC+AM.
如图,在△ABC中,D为AB边的中点,DP⊥AB交∠ACB的平分线于点P,PM⊥AC于点M,PN⊥BC交CB的延长线于点N,求证:CM=BC+AM. 如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,AM⊥BC,垂足为N,AM与DE相交于点N,S△ADE:S四边形DBCE=1:8,求AN:AM.
如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,AM⊥BC,垂足为N,AM与DE相交于点N,S△ADE:S四边形DBCE=1:8,求AN:AM.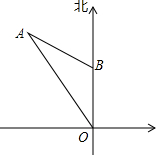 如图,某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距20
如图,某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距20